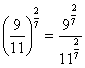A história dos problemas "O papiro de Moscou"

O papiro de Moscou foi escrito em hierático por volta de 1850 a.C., por um escriba desconhecido. Tem cerca de 8 cm de largura e 5 metros de comprimento. Na imagem vê-se a parte do papiro de Moscovo, correspondente ao problema 13, e a respectiva tradução em hieróglifos.

O papiro de Moscou foi comprado no Egito, em 1893, pelo egiptólogo V. S. Golenishchev. Originalmente foi conhecido como papiro de Golenishchev mas, quando em 1917, foi comprado pelo Museu de Belas Artes de Moscou (Pushkin), passou a ser conhecido por papiro de Moscou. O papiro contém 25 problemas, mas devido ao seu estado de degradação é impossível interpretar muitos deles. O conteúdo do Papiro de Moscou é de acordo com Clagett (1999) e Gillings (1982) o seguinte. Clique nos números para ter acesso a alguns dos problemas deste papiro. 1 Problema de aha (provavelmente a determinação de um quantidade desconhecida). 2 e 3 Problemas envolvendo barcos: o leme de um barco (pouco claro) e altura de um mastro, respectivamente. 4, 7 e 17 Envolvendo a área de um triângulo 5, 8, 9, 12, 13, 15, 16 e 22 Pesus de pães ou cerveja 6 Área de um retângulo. 10 Área de uma superfície curva de um cesto 11 Pães e cestos (pouco claro) 14 Volume de uma pirâmide truncada 18 Medidas de panos em palmos e cúbitos (pouco claro) 19 Equação linear. 20 Pesus de 1000 pães e frações de Hórus. 21 Mistura de pão para oferta 23 Cálculo do trabalho de um sapateiro (pouco claro) 24 Intercâmbios de pães e cerveja 25 Problema que dá origem à equação 2x + x =

A história dos problemas"Papiro de Berlim"

Papiro de Berlim
O papiro de Berlim data, aproximadamente, de 1800 a.C. e encontra-se no Museu Staatliche, em Berlim.
O papiro de Berlim foi comprado por A. H. Rhind, em Luxor, em 1850, na mesma altura que o papiro de Rhind, mas encontrava-se em mau estado e só foi analisado e restaurado cerca de 50 anos mais tarde por Schack-Schackenburg. O papiro de Berlim encontra-se, ainda assim, parcialmente estragado. Neste papiro aparece pela primeira a solução de uma equação do 2.º grau. Dois dos seus problemas, apresentados a seguir, dão origem a um sistema de duas equações, sendo uma delas uma equação do 2.º grau. Na notação atual os sistemas de equações envolvidos nos problemas são: x2 + y2 = 100 e 4x - 3 y = 0 (Problema 1) x2 + y2 = 400 e 4x - 3 y = 0 (Problema 2) Problema (1) É te dito ... a área de um quadrado de 100 [cúbitos quadrados] é igual à de dois quadrados mais pequenos. O lado de um dos quadrados é ½ + ¼ o lado o outro. Diz-me quais são os lados dos dois quadrados desconhecidos. Resolução: Toma sempre o quadrado de lado 1. Então o lado do outro é ½ + 2/4. Multiplica-os por ½ + 2/4. Dá ½ + 1/16, área do quadrado pequeno. Depois juntos estes quadrados têm uma área de 1 + ½ + 1/16. Tira a raiz quadrada de 1 + ½ + 1/16. Que é 1 + ¼. Tira a raiz quadrada de 100 cúbitos. Que é 10. Divide estes 10 por 1 + ¼. Dá 8, o lado de um quadrado. Calcula ½ + ¼ de 8. Dá 6, o lado do outro quadrado. (citado por Gillings) Problema (2) É te dito ... a área de um quadrado de 400 [cúbitos quadrados] é igual à de dois quadrados mais pequenos. 1 + ½ do lado de um dos quadrados é o dobro do lado do outro. Diz-me quais são os lados dos dois quadrados desconhecidos

A história dos problemas"O papiro do Cairo"

O papiro do Cairo, que se encontra atualmente no museu do Cairo, data, provavelmente, do século III a.C. e está escrito em demótico. Foi descoberto em Tuna el Geber em 1938/39. Contém 22 fragmentos que combinados dão um papiro que deveria ter 2 metros de comprimento por 35 cm de largura. O papiro contém 40 problemas, distribuídos por 20 colunas e na sua parte de trás está o código legal de Hermopolis.
Alguns dos seus problemas revelam uma forte influência de textos Babilónios, entre estes estão os que envolvem o teorema de Pitágoras.

Clique nos números para ter acesso a alguns dos problemas deste papiro.

1	Ilegível
2 e 3	Divisão de 100 por 17+2/3 e por 15+2/3, respectivamente
4 e 5	Problemas envolvendo séries de frações unitárias. Determinação do que deve ser adicionado a 1/210 para obter 1/120 e do que deve ser adicionado a 1/510 para obter 1/480, respectivamente
6	Ilegível
7 a 18	Problemas relacionados com as medidas de panos de velas, que envolvem "equações do 2.º grau"
19 a 21	Não totalmente legíveis, provavelmente envolvendo o cálculo de juros
22	Falta o bocado do papiro referente a este problema
23	Um exercício aparentemente envolvendo o cálculo da metade de frações
24 a 31	Problemas envolvendo o "Teorema de Pitágoras"
32 a 40	Problemas envolvendo áreas e volumes

A história dos problemas "Papiro de Rhind"

O papiro de Rhind está escrito em hierático, da direita para a esquerda, tem 32 cm de largura por 513 cm de comprimento. É datado de cerca de 1650 a.C., embora no texto seja referido que foi copiado de um manuscrito, de cerca de, 200 anos antes.

O papiro tem o nome do escocês Alexander Henry Rhind que o comprou, por volta de 1850, em Luxor, no Egipto. É também designado por papiro de Ahmes, o escriba egípcio que o copiou. Encontra-se atualmente no Museu Britânico.

O papiro contém uma série de tabelas e 84 problemas e as suas soluções. Eis uma listagem das suas tabelas e problemas:

Cálculos que mostram 2 dividido por cada um dos números ímpares de 3 a 101.
Uma tabela contendo os resultados da divisão de cada número de 1 a 9 por 10.
1 a 6		Divisão de 1, 2, 6, 7, 8 e 9 pães por 10 homens.
7 a 20		Multiplicação de diferentes frações por 1 + 1/2 + 1/4 ou 1 + 2/3 + 1 /3 21-23: Subtrações: 1 - (2/3 + 1/15), 1 - (2/3 + 1/30) e 2/3 - (1/4 + 1/8 + 1/10 + 1/30 + 1/45).
24 a 29		Problemas de quantidades, envolvendo equações do 1.º grau com uma incógnita, resolvidas pelo método da falsa posição.
30 a 34		Problemas semelhantes aos anteriores, mas mais complicados (envolvendo frações) e resolvidos pelo método da divisão.
35 a 38		Problemas de hekat (medida de capacidade), envolvendo equações do 1.º grau com uma incógnita mas ainda mais complexas que as anteriores, resolvidos pelo método da falsa posição.
39		Divisão de pães.
40		Divisão de pães envolvendo progressões aritméticas.
41 a 43		Volumes de contentores cilíndricos de cereais.
44 a 46		Volumes de contentores paralelepipédicos de cereais.
47		Tabela das frações de 1 hekat, como frações do olho de Horus.
48 a 53		Áreas de triângulos, rectângulos, trapézios e círculos.
54 e 55		Divisão relacionada com área.
56 a 60		Problemas relacionados com pirâmides (sekeds, alturas e bases)
61 e 61B		Tabela de uma regra para encontrar 2/3 de números ímpares e fracções unitárias.
62		Problema de proporções, sobre metais preciosos e os seu peso.
63 e 65		Divisão proporcional de pães por um número de homens.
64		Problema envolvendo uma progressão aritmética.
66		Divisão de gordura.
67		Proporção de gado devido a imposto.
68		Divisão proporcional de cereais entre grupos de homens.
69 a 78		Problemas de pesus de pão e cerveja. Proporção inversa.
79		Progressão geométrica de razão 7.
80 e 81		Tabelas das fracções do olho de Horus.
82 a 84		Problemas (pouco claros) sobre a quantidade de comida de vários animais domésticos, como gansos e outras aves

Grandes Matemáticos

Biografia

Euclides (c. 330 a. C. - 260 a. C.) nasceu na Síria e estudou em Atenas. Foi um dos primeiros geómetras e é reconhecido como um dos matemáticos mais importantes da Grécia Clássica e de todos os tempos.
Muito pouco se sabe da sua vida. Sabe-se que foi chamado para ensinar Matemática na escola criada por Ptolomeu Soter (306 a. C. - 283 a. C.), em Alexandria, mais conhecida por "Museu". Aí alcançou grande prestígio pela forma brilhante como ensinava Geometria e Álgebra, conseguindo atrair para as suas lições um grande número de discípulos. Diz-se que tinha grande capacidade e habilidade de exposição e algumas lendas caracterizam-no como um bondoso velho.

Conta-se que, um dia, o rei lhe perguntou se não existia um método mais simples para aprender geometria e que Euclides respondeu: "Não existem estradas reais para se chegar à geometria".

Outro episódio sobre Euclides refere-se a um dos seus discípulos, o qual, resolvendo ser espirituoso, depois de aprender a primeira proposição de geometria lhe perguntou qual o lucro que lhe poderia advir do estudo da geometria. Nesse momento, Euclides - para quem a geometria era coisa séria - chamou um escravo, passou-lhe algumas moedas e ordenou que as entregasse ao aluno: "já que deve obter um lucro de tudo o que aprende".

Euclides é exemplo do "Puro Homem da Ciência", que se dedica à especulação pelo gosto do saber, independentemente das suas aplicações materiais.

Obras

Embora se tenham perdido mais de metade dos seus livros, ainda restaram, para felicidade dos séculos vindouros, os treze famosos livros que constituem os Elementos (Stoicheia). Publicados por volta de 300 a. C., aí está contemplada a aritmética, a geometria e a álgebra.

Muitos outros textos lhe são atribuídos, dos quais se conhecem alguns títulos:

• Divisões de superfícies,

• Data ( continha aplicações da álgebra à geometria numa linguagem estritamente geométrica),

• Pseudaria,

• Tratado sobre Harmonia,

• A Divisão (continha muito provavelmente 36 proposições relativas à divisão de configurações planas),

• Os Dados (formavam um manual de tabelas, servindo como guia de resolução de problemas, com relação entre medidas lineares e angulares num círculo dado),

• Óptica (seria um estudo da perspectiva e desenvolveria uma teoria contrária à de Aristóteles, segundo a qual é o olho que envia os raios que vão até ao objecto que vemos e não o inverso).

• Os fenómenos (celestes) (pensa-se que Euclides discorreria sobre Geometria esférica para utilização dos astrónomos),

• Porismos (um dos mais lamentáveis desaparecimentos, este livro poderia conter aproximações à Geometria Analítica).

O trabalho de Euclides é tão vasto que alguns historiadores não acreditavam que fosse obra de um só homem. Os trabalhos matemáticos que chegaram até nós foram inicialmente traduzidos para árabe, depois para latim, e a partir destes dois idiomas para outras línguas europeias.

Embora alguns conceitos já fossem conhecidos anteriormente à sua época, o que impossibilita uma análise completa da sua originalidade, pode-se considerar o seu trabalho genial. Ao recolher tudo o que então se conhecia, sistematiza os dados da intuição e substitui imagens concretas por noções abstractas, para poder raciocinar sem qualquer apoio intuitivo.

EQUAÇÕES LITERAIS

EQUAÇÕES LITERAIS

As equações do 2º grau na variável x que possuem alguns coeficientes ou alguns termos independentes indicados por outras letras são denominadas equações literais.

As letras que aparecem numa equação literal, excluindo a incógnita, são denominadas parâmetros.

Exemplos:

ax²+ bx + c = 0 incógnita: x

parâmetro: a, b, c

ax² - (2a + 1) x + 5 = 0 incógnita: x

parâmetro: a

Equações literais incompletas

A resolução de equações literais incompletas segue o mesmo processo das equações numéricas.

Observe os exemplos:

• Resolva a equação literal incompleta 3x² - 12m²=0, sendo x a variável.

Solução

3x² - 12m² = 0

3x² = 12m²

x² = 4m²

x=

Logo, temos:

• Resolva a equação literal incompleta my²- 2aby=0,com m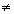0, sendo y a variável.

Solução

my² - 2aby = 0

y(my - 2ab)=0

Temos, portanto, duas soluções:

y=0

ou

my - 2ab = 0 my = 2ab y=

Assim:

Na solução do último exemplo, teríamos cometido um erro grave se tivéssemos assim resolvido:

my² - 2aby= 0

my² = 2aby

my = 2ab

Desta maneira, obteríamos apenas a solução .

O zero da outra solução foi "perdido" quando dividimos ambos os termos por y.

Esta é uma boa razão para termos muito cuidado com os cancelamentos, evitando desta maneira a divisão por zero, que é um absurdo.

Equações literais completas

As equações literais completas podem ser também resolvidas pela fórmula de Bhaskara:

Exemplo:

Resolva a equação: x² - 2abx - 3a²b², sendo x a variável.

Solução

Temos a=1, b = -2ab e c=-3a²b²

Portanto:

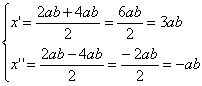
Assim, temos: V= { - ab, 3ab}.

Humor

Racionalização de denominadores

Racionalização de denominadores

Considere a fração: que seu denominador é um número irracional.

Vamos agora multiplicar o numerador e o denominador desta fração por , obtendo uma fração equivalente:

Observe que a fração equivalente possui um denominador racional.

A essa transformação, damos o nome de racionalização de denomindores.

A racionalização de denominadores consiste, portanto, na obtenção de um fração com denominador racional, equivalente a uma anterior, que possuía um ou mais radicais em seu denominador.

Para racionalizar o denominador de uma fração devemos multiplicar os termos desta fração por uma expressão com radical, denominado fator racionalizante, de modo a obter uma nova fração equivalente com denominador sem radical.

Principais casos de racionalização:

1º Caso: O denominador é um radical de índice 2: Exemplos:

é o fator racionalizante de , pois . = = a

2º Caso: O denominador é um radical de índice diferente de 2. Exemplos:

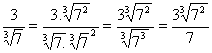
é o fator racionalizante de

é o fator racionalizante de

é o fator racionalizante de

é o fator racionalizante de

Potência com expoente racional

Observe as seguintes igualdades:

ou

Igualmente podemos transformar uma potência com expoente fracionário em um radical.

De modo eral, definimos:

, com a R,m,n, N, a >0, n>0, m>0

Podemos também transformar um radical com expoente fracionário:

Propriedade das potências com expoentes racionais

As propriedades das potências com expoentes racionais são as mesmas para os expoentes inteiros.

Sendo a e b números reais e positivos e os expoentes números racionais, temos que:

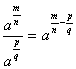
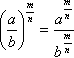
Exemplo: