Piadas Matemáticas

O estudante, cansado de assistir aulas de Matemática, levanta a mão e confronta o professor:
- Eu acho que a gente nunca vai usar essas coisas na vida real.
O professor sorri e responde:
- É verdade, especialmente se a sua vida real não for nada mais que servir café na lanchonete.

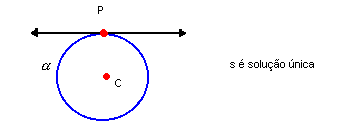
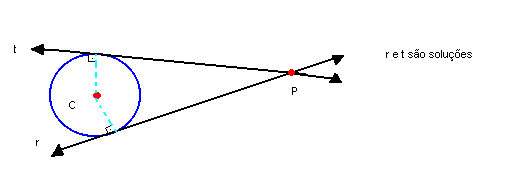
Geometria Analítica: Circunferência Condições de tangência entre reta e circunferência Dados uma circunferência e um ponto P(x, y) do plano, temos: a) se P pertence à circunferência, então existe uma única reta tangente à circunferência por P b) se P é exterior à circunferência, então existem duas retas tangentes a ela por P c) se P é interior à circunferência, então não existe reta tangente à circunferência passando pelo ponto P

Geometria Analítica: Circunferência
Fonte:http://www.somatematica.com.br/
   

Condições de tangência entre reta e circunferência
   Dados uma circunferência e um ponto P(x, y) do plano, temos:
a) se P pertence à circunferência, então existe uma única reta tangente à circunferência por P

b) se P é exterior à circunferência, então existem duas retas tangentes a ela por P

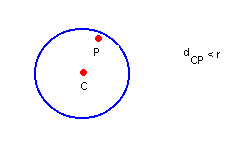
c) se P é interior à circunferência, então não existe reta tangente à circunferência passando pelo ponto P

Circunferência

Geometria Analítica: Circunferência
Fonte:http://www.somatematica.com.br/
   

Posição de uma reta em relação a uma circunferência
   Dadas uma reta s: Ax + Bx + C = 0 e uma circunferência de equação
 ( x - a)² + ( y - b)² = r², vamos examinar as posições relativas entre s e :

    Também podemos determinar a posição de uma reta em relação a uma circunferência calculando a distância da reta ao centro da circunferência. Assim, dadas a reta s: Ax + By + C = 0 e a circunferência :
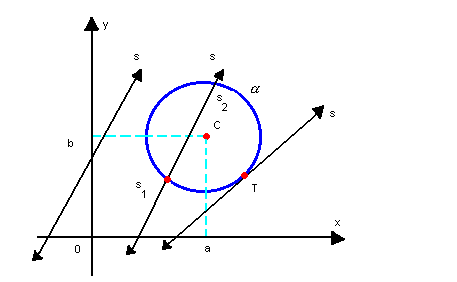
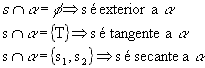
(x - a)² + ( y - b )² = r², temos:

Assim:

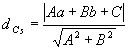
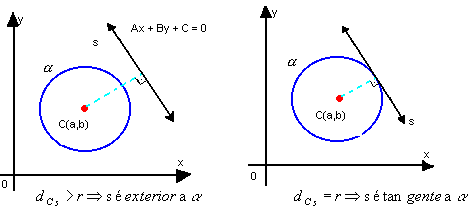
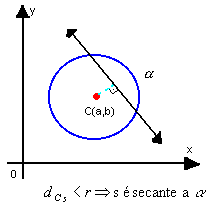
Determinação do centro e do raio da circunferência, dada a equação geral
Fonte: http://www.somatematica.com.br/

   Dada a equação geral de uma circunferência, utilizamos o processo de fatoração de trinômio quadrado perfeito para transformá-la na equação reduzida e , assim, determinamos o centro e o raio da circunferência.

   Para tanto, a equação geral deve obedecer a duas condições:

• os coeficientes dos termos x² e y² devem ser iguais a 1;
• não deve existir o termo xy.

   Então, vamos determinar o centro e o raio da circunferência cuja equação geral é x² + y² - 6x + 2y - 6 = 0.

   Observando a equação, vemos que ela obedece às duas condições. Assim:

• 1º passo: agrupamos os termos em x e os termos em y e isolamos o termo independente

x² - 6x + _ + y² + 2y + _ = 6

• 2º passo: determinamos os termos que completam os quadrados perfeitos nas variáveis x e y, somando a ambos os membros as parcelas correspondentes

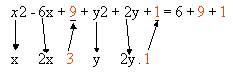
• 3º passo: fatoramos os trinômios quadrados perfeitos

( x - 3 ) ² + ( y + 1 ) ² = 16

• 4º passo: obtida a equação reduzida, determinamos o centro e o raio

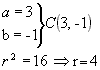
Posição de um ponto em relação a uma circunferência

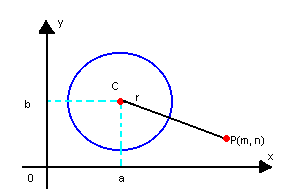
   Em relação à circunferência de equação ( x - a )² + ( y - b )² = r², o ponto P(m, n) pode ocupar as seguintes posições:

a) P é exterior à circunferência
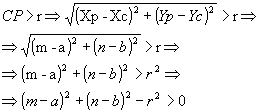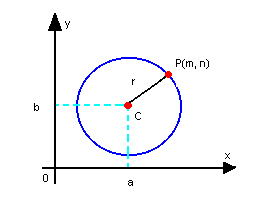
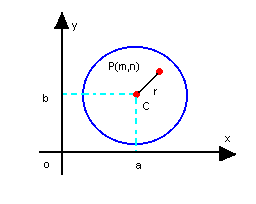
b) P pertence à circunferência
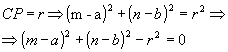c) P é interior à circunferência

    Assim, para determinar a posição de um ponto P(m, n) em relação a uma circunferência, basta substituir as coordenadas de P na expressão ( x - a )² + ( y - b )² - r²:

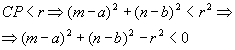• se ( m - a)² + ( n - b)² - r² > 0, então P é exterior à circunferência;
• se ( m - a)² + ( n - b)² - r² =    0, então P pertence à circunferência;
• se ( m - a)² + ( n - b)² - r² < 0, então P é interior à circunferência.

Circunferência

Geometria Analítica: Circunferência
Fonte:  http://www.somatematica.com.br/

 
Equações da circunferência
Equação reduzida
    Circunferência é o conjunto de todos os pontos de um plano eqüidistantes de um ponto fixo, desse mesmo plano, denominado centro da circunferência:

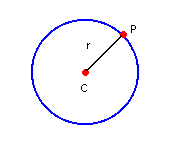
   Assim, sendo C(a, b) o centro e P(x, y) um ponto qualquer da circunferência, a distância de C a P(d_CP) é o raio dessa circunferência. Então:

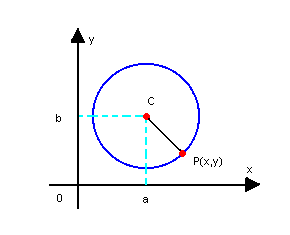
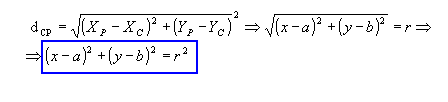
    Portanto, (x - a)² + (y - b)² =r² é a equação reduzida da circunferência e permite determinar os elementos essenciais para a construção da circunferência: as coordenadas do centro e o raio.

Observação: Quando o centro da circunfer6encia estiver na origem ( C(0,0)), a equação da circunferência será x² + y² = r² .

Equação geral

   Desenvolvendo a equação reduzida, obtemos a equação geral da circunferência:

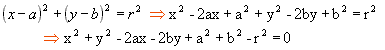
    Como exemplo, vamos determinar a equação geral da circunferência de centro C(2, -3) e raio r = 4.

   A equação reduzida da circunferência é:

( x - 2 )² +( y + 3 )² = 16

   Desenvolvendo os quadrados dos binômios, temos:

Circunferência