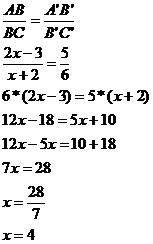Sistemas de equação do 1º grau

Os sistemas de equação são ferramentas muito comuns na resolução de problemas em várias áreas (matemática, química, física, engenharia,...) e aparecem sempre em concursos e exames, como é o caso do vestibular. Os sistemas, geralmente, são resolvidos com uma certa facilidade o que causa muitas vezes uma desatenção, por parte do aluno, já que ele não tem dificuldade para encontrar a solução do sistema. Mas ele esquece que a dificuldade está na armação e principalmente na solução final da questão. Os sistemas são ferramentas que mesmo funcionando necessitam de alguém que saiba o construir com elas.

II – MÉTODOS DE RESOLUÇÃO DE SISTEMAS DE EQUAÇÕES DO 1º GRAU

Além de saber armar o sistema é bom saber fazer a escolha pelo método mais rápido de resolução.
Vou apresentar três métodos sendo que o mais utilizado é o método da adição.

1º) método da adição

Este método consiste em deixar os coeficientes de uma incógnita opostos. Desta forma, somando-se membro a membro as duas equações recai-se em um equação com uma única incógnita.

EXEMPLO: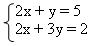

1º passo: vamos multiplicar a primeira linha por -1 para podermos cortar –2x com 2x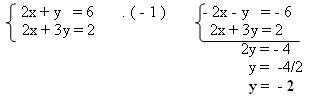

2º passo: Substituir y = - 2, em qualquer um das equações acima e encontrar o valor de x.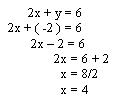

3º passo: dar a solução do sistema.

S = { (4, -2) }

2º) método da substituição

Este método consiste em isolar uma incógnita numa equação e substituí-la na outra equação do sistema dado, recaindo-se numa equação do 1º grau com uma única incógnita.

EXEMPLO: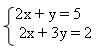

1º passo: vamos isolar o y na primeira equação para podermos substituir na Segunda equação.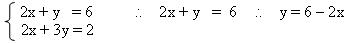

2º passo: Substituir y = 6 – 2x, na segunda equação para encontrar o valor de x.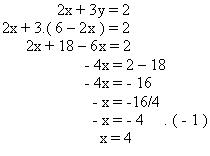

3º passo: Substituir x = 4 em y = 6 – 2x, para encontrar o valor de y.

y = 6 – 2x
y = 6 – 2.4
y = 6 – 8
y = -2

4º passo: dar a solução do sistema.

S = { (4, -2) }

Teorema de Tales

Tales de Mileto foi um importante filósofo, astrônomo e matemático grego que viveu antes de Cristo. Ele usou seus conhecimentos sobre Geometria e proporcionalidade para determinar a altura de uma pirâmide. Em seus estudos, Tales observou que os raios solares que chegavam à Terra estavam na posição inclinada e eram paralelos, dessa forma, ele concluiu que havia uma proporcionalidade entre as medidas da sombra e da altura dos objetos, observe a ilustração:

Com base nesse esquema, Tales conseguiu medir a altura de uma pirâmide com base no tamanho da sua sombra. Para tal situação ele procedeu da seguinte forma: fincou uma estaca na areia, mediu as sombras respectivas da pirâmide e da estaca em uma determinada hora do dia e estabeleceu a proporção:

O Teorema de Tales pode ser determinado pela seguinte lei de correspondência:

“Feixes de retas paralelas cortadas ou intersectadas por segmentos transversais formam segmentos de retas proporcionalmente correspondentes”.

Para compreender melhor o teorema observe o esquema representativo a seguir:

Pela proporcionalidade existente no Teorema, temos a seguinte situação:

Exemplo 1
Aplicando a proporcionalidade existente no Teorema de Tales, determine o valor dos segmentos AB e BC na ilustração a seguir:

AB = 2x – 3
BC = x + 2
A’B’ = 5
B’C’ = 6

Determinando o valor de x:

AB = 2x – 3 → 2*4 – 3 = 5
BC = x + 2 → 4 + 2 = 6

Exemplo 2
Determine o valor de x na figura a seguir: