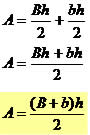Veja alguns exemplos e as explicações passo a passo de como encontrar a solução desse tipo de problema e de como a fração pode ser encontrada em situações problemas.
Exemplo 1:
Em certo país, os trabalhadores recebem dois salários mínimos em dezembro: o salário normal e o 13º salário. Se a pessoa trabalhou os 12 meses do ano, os dois salários serão iguais. Se a pessoa trabalhou uma fração do ano, o 13º salário corresponderá a essa fração do salário normal. Se o salário normal de uma pessoa é 516 reais e ela trabalhou 7 meses nesse ano, quanto ela vai receber de 13º salário?
Resolução:
Esse trabalhador não trabalhou o ano inteiro, de 12 meses do ano ele trabalhou 7 meses. A fração que corresponde ao tempo que ele trabalhou é
informou que o valor recebido no 13º salário é a mesma fração do tempo trabalhado, podemos escrever que ele irá receber
reais, para descobrir quanto ele irá receber no 13º salário devemos encontrar:
Portanto, o salário que o trabalhador irá receber no seu 13º salário será de 301 reais que corresponde a 7 meses trabalhados durante o ano.
Exemplo 2:
João Carlos é operário e seu salário é apenas 520 reais por mês. Gasta
e
foram gastos com remédios. Sobrou dinheiro?
Resolução:
Para saber se o salário de João Carlos foi suficiente para pagar todas as suas despesas é preciso encontrar o valor que ele gastou com o pagamento do aluguel, com a alimentação e com os remédios. Então, veja:
1 de 520 = 520 : 4 x 1 = 130.
4
2 de 520 = 520 : 5 x 2 = 104 x 2 = 208
5
3 de 520 = 520 : 8 x 3 = 195.
8
Concluímos que ele gastou com essas despesas um total de 130+208+195 = 533 reais. Portanto, não sobrou nada de seu salário, pelo contrário, ele ficou devendo, pois suas despesas foram 13 reais a mais que seu salário.