ALUNOS COPIAR E RESOLVER OS EXERCÍCIOS NO CADERNO PELA VISUALIZAÇÃO !!
Abraços Betão
É papel do educador combater o medo de errar que inibe, as possibilidades de realização e satisfação. "Prof. Marcondes Diniz Martins"
Consideremos o prisma como um sólido geométrico formado pelos seguintes elementos: base, altura, vértices, arestas e faces laterais. Os prismas podem apresentar diversas formas, mas algumas características básicas definem esse sólido geométrico. Por exemplo, o número de faces do prisma será exatamente igual ao número de lados do polígono que constitui suas bases (superior e inferior), dessa forma, sua classificação quanto ao número de lados pode ser:
Triangular – base constituída de triângulos.
Quadrangular – base constituída de quadriláteros.
Pentagonal – base constituída de pentágonos.
Hexagonal – base constituída de hexágonos.
Heptagonal – base constituída de heptágonos.
Octogonal – base constituída de octógonos.
Os prismas também podem ser classificados como retos ou oblíquos. Os prismas retos são aqueles em que a aresta lateral forma com a base um ângulo de 90º, os oblíquos são aqueles em que as arestas formam ângulos diferentes de 90º.
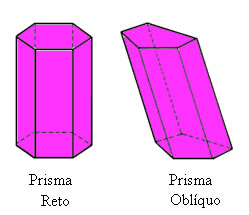
Todos os prismas possuem área da base, área lateral, área total e volume. Todas essas medidas dependem do formato do polígono que se encontra nas bases; por exemplo, os prismas acima possuem em sua base um pentágono, portanto, para calcularmos a área dessa base devemos determinar a área do pentágono. No caso do prisma pentagonal reto, as faces laterais constituem retângulos e a do prisma oblíquo é formada por paralelogramos.
A área total de um prisma é calculada somando a área lateral e o dobro da área da base. E o volume é determinado calculando a área da base multiplicada pela medida da altura.
Observe alguns exemplos de prismas:
Prisma Triangular Reto
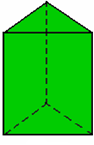
Prisma Hexagonal Reto
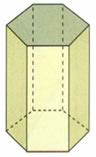
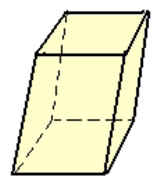
Prisma Pentagonal Oblíquo

Prisma Quadrangular Oblíquo
A área do círculo é diretamente proporcional ao raio, que é a distância entre o centro e a sua extremidade. Para calcularmos a área do círculo, utilizamos a expressão matemática que relaciona o raio e a letra grega π (pi), que corresponde a, aproximadamente, 3,14.
A = π * r²
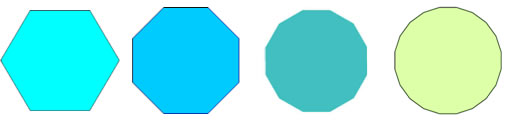
O círculo é determinado de acordo com o aumento do número de lados de um polígono. Quanto mais lados um polígono apresenta, mais ele se assemelha a um círculo. Observe as figuras na seguinte ordem: hexágono (6 lados), octógono (8 lados), dodecágono (12 lados) e icoságono (20 lados).
Vamos determinar a área de algumas regiões circulares.
Exemplo 1
Determine quantos metros quadrados de grama são necessários para preencher uma praça circular com raio medindo 20 metros.

A = π * r²
A = 3,14 * 20²
A = 3,14 * 400
A = 1256 m²
Serão necessários 1256 m² de grama.
Exemplo 2
Determine a área da região em destaque representada pela figura a seguir. Considerando que a região maior possui raio medindo 10 metros, e a região menor, raio medindo 3 metros.






Na combinação simples, a ordem dos elementos no agrupamento não interfere. São arranjos que se diferenciam somente pela natureza de seus elementos. Portanto, se temos um conjunto A formado por n elementos tomados p a p, qualquer subconjunto de A formado por p elementos será uma combinação, dada pela seguinte expressão:

Por exemplo, considere um conjunto com seis elementos que serão tomados dois a dois:
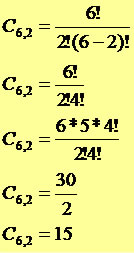
Uma importante aplicação de combinação simples é nas loterias, megassena, quina entre outras. A megassena consiste em uma cartela de 60 números dentre os quais devemos acertar 6 (prêmio principal), portanto temos uma combinação onde n = 60 e p = 6, sessenta números tomados seis a seis.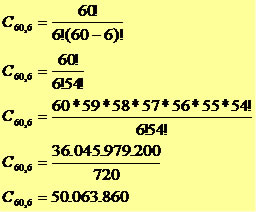
Na megassena existem 50.063.860 combinações, caso sejam tomadas seis a seis.
Em um curso de língua estrangeira estudam trinta alunos. O coordenador do curso quer formar um grupo de três alunos para realizar um intercâmbio em outro país. Quantas possíveis equipes podem ser formadas?
Resolução
O número de possíveis grupos pode ser dado pela expressão:

Poderão ser formadas 4060 equipes.
A análise combinatória estuda dois tipos de agrupamentos: Arranjos e combinações. Sendo que diferem em arranjos simples, combinações simples.
Arranjos são agrupamentos que a ordem dos seus elementos faz a diferença, por exemplo, os números de três algarismos formados pelos elementos {1,2 e 3} são:
312, 321, 132, 123, 213, 231
Esse agrupamento é um arranjo, pois a ordem dos elementos 1, 2 e 3 diferem. E é considerado simples, pois os elementos não se repetem.
Para que tenhamos arranjos simples é preciso ter um conjunto de elementos distintos com uma quantidade qualquer de elementos, sendo que os arranjos simples formados irão possuir n elementos, sendo que essa quantidade será igual ou menor que a quantidade de elementos do conjunto.
Veja o exemplo abaixo:
Dado o conjunto B = {5,6,7}, veja os possíveis agrupamentos formados com 2 elementos de B.
Então, os agrupamentos formados com 2 elementos do conjunto b são: 56,57,65,67,75,76. Esse agrupamento é formado por arranjos simples pelos elementos do conjunto B.
Nesse exemplo percebemos que é possível formar 6 arranjos, essa quantidade pode ser representada da seguinte forma: A3,2 (três elementos distintos formados de dois a dois). Utilizando o processo do princípio fundamental da contagem, calculamos a quantidade de elementos:
A3,2 = 3 . 2 . 1 = 6
Se em um agrupamento compararmos os arranjos simples formados perceberemos que eles se diferem de duas maneiras diferentes: pela ordem de seus elementos ou pela natureza de seus elementos. Por exemplo:
Se compararmos os arranjos 56 e 65 do exemplo anterior, perceberemos que eles são diferentes pela ordem dos seus elementos.
Se compararmos os arranjos 75 e 76 do exemplo anterior, perceberemos que eles são diferentes pela natureza de seus elementos, pois são diferentes.
Considerando n a quantidade de elementos de um conjunto qualquer e p um número natural menor ou igual a n. p será a classe ou a ordem do arranjo. Indicado da seguinte forma: A n , p
A fórmula geral utilizada no cálculo da quantidade de arranjos simples é:
Exemplo 2:
Quantas “palavras” (com sentido ou não) de 5 letras distintas podemos formar com as 20 primeiras letras do nosso alfabeto?
Não é necessário montar todas os arranjos possíveis para saber a sua quantidade, basta aplicar a fórmula
A n , p = n!
(n – p)!
Sendo que o conjunto é formado por 20 elementos (n = 20) que serão unidos de 5 em 5 (p = 5). Substitua a fórmula.
Portanto, a quantidade de arranjos formados com as 20 primeiras letras do nosso alfabeto unidas de 5 em 5 é 1860480.

Exemplo 2
De quantas maneiras distintas podemos organizar as modelos Ana, Carla, Maria, Paula e Silvia para a produção de um álbum de fotografias promocionais?
Resolução:
Note que o princípio a ser utilizado na organização das modelos será o da permutação simples, pois formaremos agrupamentos que se diferenciarão somente pela ordem dos elementos.
P = n!
P = 5!
P = 5*4*3*2*1
P = 120
Portanto, o número de posições possíveis é 120.
Exemplo 3
De quantas maneiras distintas podemos colocar em fila indiana seis homens e seis mulheres:
a) em qualquer ordem
Resolução
Podemos organizar as 12 pessoas de forma distinta, portanto utilizamos
12! = 12*11*10*9*8*7*6*5*4*3*2*1 = 479.001.600 possibilidades
b) iniciando com homem e terminando com mulher
Resolução
Ao iniciarmos o agrupamento com homem e terminarmos com mulher teremos:
Seis homens aleatoriamente na primeira posição.
Seis mulheres aleatoriamente na última posição.


Algebrista italiano nascido em Bologna, o mais importante da história da matemática da Itália, pioneiro no estudo sobre os números imaginários: sua principal publicação sobre álgebra, Álgebra, composto de cinco volumes, e com os livros IV e o V estivessem incompletos, só foi editada (1573) no ano seguinte à sua morte.
O mais velho dos seis filho de Antonio Mazzoli, cuja família havia chegado a Bologna no século anterior (1443). Com o controle da cidade tomado de Giovanni II Bentivoglio pelo papa Júlio II (1506), seu pai envolveu-se numa tentativa de retomado do poder pelos antigos governantes, os Bentivoglios, porém foram derrotados (1508), os cabeças dos Bentivoglios executados, sua família exilada e todos os bens confiscados.
Após vários anos de exílio os Mazzoli foram perdoados e Antonio Mazzoli pode voltar para Bologna, recuperar as propriedades da família e se tornou um bem-sucedido negociante no ramo de lãs. Embora não tenha tido educação universitária, mudou seu nome para Bombelli, na tentativa de disfarçar sua descendência e, depois de várias atividades menores, passou a trabalhar para um nobre romano, Alessandro Rufini, futuro bispo de Melfi.
Neste período interessou-se por matemática e envolveu-se na coqueluche da época que era a solução das cúbicas e quárticas, envolvendo del Ferro, Fior, Tartaglia, Cardano e Ferrari, teminando com o encontro entre Ferrari e Tartaglia, em Milão (1548). Estudou matemática com o professor Pier Francesco Clementi (1548), que era ligado ao papado, e quando seu patrão adquiriu os direitos sobre a região do Val di Chiana (1549), que passara a pertencer aos Estados Papais, ele foi encarregado de demarcar as fronteiras (1551-1555), quando teve de interromper os serviços por causa de uma reclamação dos vizinhos fronteiriços. Foi nesse período, enquanto aguardava o recomeço das demarcações, que resolveu escrever seu famoso livro de álgebra, partindo dos estudos de Cardano.
Ele começou a escrevê-lo quando o trabalho em Val di Chiana ainda estava suspenso (1557). Quando o trabalho recomeçou (1560) o livro ainda estava sendo escrito. Após uma visita ao professor da Universidade de Roma, Antonio Maria Pazzi, este lhe mostrou um manuscrito de Diofanto, Aritmética, que o deixou encantado e os dois resolveram fazer uma tradução, porém no seu livro III, a despeito de 143 dos 272 problemas existentes serem baseados nos escritos de Diofanto, ele não deu os devidos créditos ao grande matemático grego.
Desafortunadamente morreu, provavelmente em Roma, antes de completar os livros IV e V, porém sua criação mudou a história da álgebra. O pesquisador Bortolotti encontrou seus manuscritos numa biblioteca de Bologna (1923) e republicou seus cinco livros (1929), uma contribuição fundamental para o estudo dos números complexos. Em sua álgebra ele escreveu por exemplo:
MAIS vezes MAIS é igual a MAIS;
MENOS vezes MENOS é igual a MAIS;
MAIS vezes MENOS é igual a MENOS;
MENOS vezes MAIS é igual a MENOS;
+RAIZ QUADRADA DE -n . +RAIZ QUADRADA DE -n = - n;
+RAIZ QUADRADA DE -n . - RAIZ QUADRADA DE -n = +n;
- RAIZ QUADRADA DE -n . +RAIZ QUADRADA DE -n = +n;
- RAIZ QUADRADA DE -n . - RAIZ QUADRADA DE -n = - n.
Exemplos das notações empregadas por Bombelli
Em seu trabalho descreveu a adição, subtração e multiplicação dos números complexos e forneceu a correta solução das cúbicas empregando a fórmula Cardan-Tartaglia sempre que ocorressem situações com raízes quadradas de números negativos. Outra admirável contribuição do autor foi a larga, prática e renovadora notação empregando símbolos em suas expressões matemáticas. Com menos projeção também exerceu engenharia e arquitetura, principalmente em obras de pontes e drenagem de pântanos.
Tabela traduzida do site TURNBULL WWW SERVER:
http://www-history.mcs.st-andrews.ac.uk/

Em seu gabinete de trabalho, iluminado pela luz de uma vela, Robert Recorde estava debruçado sobre uma folha repleta de números e letras, com uma pena na mão. Tomando sua decisão, mergulhou a pena no tinteiro e desenhou um tracinho horizontal. Bem acima, desenhou um segundo traço do mesmo comprimento, rigorosamente paralelo.
____
____
Colocou a pena sobre a mesa, pegou a folha e ergueu-a esticando bem os braços. Ficou satisfeito com o sinal que havia criado. E com razão, visto que diante dele estava o que se tornaria o mais célebre sinal da matemática, o de igualdade. Pouco depois, quando o sinal já circulava no mundo dos matemáticos, interrogaram Recorde sobre o porquê da escolha. Ele justificava:
"Se escolhi um par de paralelas, é porque elas são duas linhas gêmeas, e nada é mais semelhante que dois gêmeos".
Não sabe-se exatamente os tópicos que ele estudou, mas sabe-se que obteve o grau de B.A. em 1531, e naquele ano foi eleito membro do All Souls College, em Oxford. Robert Recorde praticamente estabeleceu a escola inglesa de matemáticos, fazendo a introdução da álgebra na Inglaterra.
Escreveu vários livros-texto elementares, e fez isso com uma política bastante deliberada. Tinha a idéia de produzir um curso completo de instrução matemática, e escreveu esses livros na ordem na qual ele achava que deveria ser estudada em um curso de matemática. Ele queria que esse curso estivesse disponível para qualquer pessoa, e não somente para poucos homens que podiam ler em latim ou grego. Então, ele escreveu todos esses livros em inglês e, tentando usar expressões claras e simples. Para isso, introduziu novas palavras inglesas equivalentes aos termos em latim ou grego em uso na época.
As idéias de Recorde eram desenvolvidas claramente, passo a passo, com os pontos difíceis sendo guardados até que o estudante obtivesse experiência suficiente para entendê-los. Em 1543, Recorde publicou The Grounde of Artes, um livro de aritmética de bastante sucesso:
...teaching the perfect work and practice of Arithmeticke etc.
nas próprias palavras de Recorde. O livro abordava operações com números arábicos, computação com contadores, proporções, regra de três, tudo sendo estudado aritmeticamente com números naturais. Houve uma segunda e uma terceira edição em 1549 e 1550. Em 1552, Recorde publicou também uma segunda versão ampliada do The Grounde of Artes, estendendo o trabalho da primeira edição.
Em 1551, Recorde escreveu a obra Pathwaie to Knowledge, que alguns consideravam como uma versão resumida dos "Elementos" de Euclides. Foi o único dos seus livros que ele escreveu na forma de diálogo entre mestre e estudante. Ele explicava porque os teorema são verdadeiros e dava diversos exemplos para fazer com que o estudante entendesse não só o que estava sendo ensinado, mas também porque aquilo estava sendo ensinado.
Em 1556 publicou The Castle of Knowledge, onde apresentou uma elementar introdução à versão de Ptolomeu sobre astronomia. Foi, portanto, um trabalho matemático sobre a esfera, e Recorde certamente leu os trabalhos de Ptolomeu, Proclus, Sacrobosco e Oronce Fine antes de escrevê-lo.
Em relação ao sinal de igual (=), ele apareceu no seu livro The Whetstone of Witte, publicado em 1557.
A forma de uma Notação científica é: m . 10 e, onde m significa mantissa e E significa ordem de grandeza. A mantissa SEMPRE será um valor em módulo entre 1 e 10.
Transformando
Para transformar um numero grande qualquer em notação cientifica, devemos deslocar a vírgula para a esquerda até o primeiro algarismo desta forma:
200 000 000 000 » 2,00 000 000 000
note que a vírgula avançou 11 casas para a esquerda, entao em notação cientifica este numero fica: 2 . 1011.
Para com valores muito pequenos, é só mover a virgula para a direita, e a cada casa avançada, diminuir 1 da ordem de grandeza:
0,0000000586 » movendo a virgula para direita » 5,86 (avanço de 8 casas) » 5,86 . 10-8
-12.000.000.000.000 » -1,2 . 1013
Denomina-se Binômio de Newton , a todo binômio da forma (a + b)n , sendo n um número natural .
Exemplo:
B = (3x - 2y)4 ( onde a = 3x, b = -2y e n = 4 [grau do binômio] ).
Nota 1:
Isaac Newton - físico e matemático inglês(1642 - 1727).
Suas contribuições à Matemática, estão reunidas na monumental obra Principia Mathematica, escrita em 1687.
Exemplos de desenvolvimento de binômios de Newton :
a) (a + b)2 = a2 + 2ab + b2
b) (a + b)3 = a3 + 3 a2b + 3ab2 + b3
c) (a + b)4 = a4 + 4 a3b + 6 a2b2 + 4ab3 + b4
d) (a + b)5 = a5 + 5 a4b + 10 a3b2 + 10 a2b3 + 5ab4 + b5
Nota 2:
Não é necessário memorizar as fórmulas acima, já que elas possuem uma lei de formação bem definida, senão vejamos:
Vamos tomar por exemplo, o item (d) acima:
Observe que o expoente do primeiro e últimos termos são iguais ao expoente do binômio, ou seja, igual a 5.
A partir do segundo termo, os coeficientes podem ser obtidos a partir da seguinte regra prática de fácil memorização:
Multiplicamos o coeficiente de a pelo seu expoente e dividimos o resultado pela ordem do termo. O resultado será o coeficiente do próximo termo. Assim por exemplo, para obter o coeficiente do terceiro termo do item (d) acima teríamos:
5.4 = 20; agora dividimos 20 pela ordem do termo anterior (2 por se tratar do segundo termo) 20:2 = 10 que é o coeficiente do terceiro termo procurado.
Observe que os expoentes da variável a decrescem de n até 0 e os expoentes de b crescem de 0 até n. Assim o terceiro termo é 10 a3b2 (observe que o expoente de a decresceu de 4 para 3 e o de b cresceu de 1 para 2).
Usando a regra prática acima, o desenvolvimento do binômio de Newton (a + b)7 será:
(a + b)7 = a7 + 7 a6b + 21 a5b2 + 35 a4b3 + 35 a3b4 + 21 a2b5 + 7 ab6 + b7
Como obtivemos, por exemplo, o coeficiente do 6º termo (21 a2b5) ?
Pela regra: coeficiente do termo anterior = 35. Multiplicamos 35 pelo expoente de a que é igual a 3 e dividimos o resultado pela ordem do termo que é 5.
Então, 35 . 3 = 105 e dividindo por 5 (ordem do termo anterior) vem 105:5 = 21, que é o coeficiente do sexto termo, conforme se vê acima.
Observações:
1) o desenvolvimento do binômio (a + b)n é um polinômio.
2) o desenvolvimento de (a + b)n possui n + 1 termos .
3) os coeficientes dos termos eqüidistantes dos extremos , no desenvolvimento de
(a + b)n são iguais .
4) a soma dos coeficientes de (a + b)n é igual a 2n .
Fórmula do termo geral de um Binômio de Newton
Um termo genérico Tp+1 do desenvolvimento de (a+b)n é dado por
Tp+1 = Cn,p . an - p .bp (Fórmula do Termo geral de um binómio de Newton).
onde Cn,p = n! / [(n-p)! . p!] .
Obs :
1) o desenvolvimento do binómio (a + b)n é um polinómio.
2)o desenvolvimento de (a + b)n possui n + 1 termos .
3) os coeficientes dos termos equidistantes (mesma distancia) dos extremos , no desenvolvimento de (a + b)n são iguais .
4) a soma dos coeficientes de (a + b)n é igual a 2n .


Matemático e físico grego. Nascido em Siracusa-Sicília, por volta do ano 287 a.C, o seu nome é originário do grego Arkhimedes. Quando jovem muda-se para Alexandria, centro da atividade matemática, onde continua as aulas de Euclides. De volta à sua pátria, entrega-se por completo aos estudos científicos.
Segundo narração de Plutarco, general romano, refere as passagens relativas à luta travada pelos romanos para a posse da Sicília, especialmente para a conquista da cidade de Siracusa. Quando os Romanos atacaram Siracusa, Arquimedes dirige a defesa da sua cidade, para o que se serve de máquinas de guerra (catapultas, etc.). Após um longo assédio, as tropas de Marcelo entram na cidade. Segundo Plutarco, apesar das ordens de Marcelo para respeitar a vida do sábio, um soldado romano, irritado porque Arquimedes, absorto na resolução de um problema, não responde às suas intimações, mata-o. Cícero, questor da Sicília, encontra o seu túmulo, onde figura uma esfera inscrita num cilindro.
São bastantes as obras de Arquimedes que chegaram até aos nossos dias. Na matemática, destacam-se Da Esfera e do Cilindro, A Medida do Círculo, Dos Esferóides e dos Conóides e Das Linhas Espirais. Nas obras de mecânica há que citar, Do Equilíbrio dos Planos e Dos Corpos Flutuantes. Outros achados importantes, são A Quadratura da Parábola e O Método.
DEdicou-se a aritmética, mecânica e hidrostática. Atribuem-se a Arquimedes a invenção do parafuso sem fim, da espiral ou parafuso de Arquimedes (aparelho para elevar água por meio de um tubo enrolado em hélice à volta de um cilindro giratório sobre o seu eixo), de diversas combinações de roldanas para levantar pesos, da roda dentada, relação da circunferência com o diâmetro (o número pi), a quadratura da parábola, as propriedades das espirais, etc.
Há uma célebre anedota da Antiguidade relacionada com os estudos hidrostáticos de Arquimedes. Trata-se do chamado problema da coroa. Hiero, rei de Siracusa, encomenda uma coroa que paga como se fosse de ouro puro, mas posteriormente suspeita que o ourives fez mistura do ouro com prata. Arquimedes resolve o problema determinando o volume da coroa, para o que a submerge num recipiente completamente cheio de água e pesa de seguida o líquido derramado. Averigua assim a densidade da coroa e calcula a proporção de prata que o desleal ourives utiliza. Conta-se que Arquimedes inventa este procedimento quando, ao se introduzir num recipiente completamente cheio de água para se lavar, parte dela transborda. Sai então do banho a gritar Eureka! (que em grego significa «Achei!»). O clássico enunciado deste princípio, chamado de Arquimedes, é o seguinte: todo o corpo submergido num fluido experimenta um impulso de baixo para cima igual ao peso do fluído que desloca.
Formula também a teoria da alavanca simples, resumida numa frase célebre: «Dai-me um ponto de apoio e levantarei a Terra.