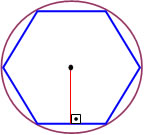
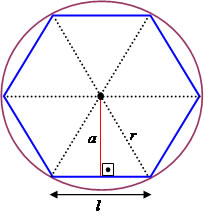
Considerando um círculo e um polígono inscrito de n lados, definimos como apótema de uma figura poligonal o segmento de reta que parte do centro da figura formando com o lado um ângulo de 90º, isto é, podemos dizer que o apótema é perpendicular ao lado do polígono.
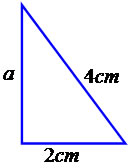
a² + 2² = 4²
a² + 4 = 16
a² = 16 – 4
a² = 12
√a² = √12
a = 2√3 cm
Exemplo 2
Determine o apótema do quadrado inscrito na circunferência e a medida do raio, sabendo que o lado do quadrado mede 10 cm.
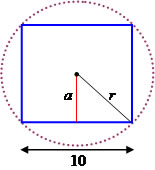

Determinando o apótema através da tangente do ângulo de 45º (360º : 8).
tg 45º = 5/a
1 = 5/a
a = 5 cm
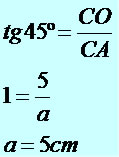
Determinando o raio através do Teorema de Pitágoras:
r² = a² + 5²
r² = 5² + 5²
r² = 25 + 25
r² = 50
√r² = √50
r = 5√2 cm
Exemplo 3
Determine a medida do apótema da pirâmide a seguir, sabendo que sua altura mede 4,8 cm e o apótema da base mede 3,6 cm.
Resolução:
O apótema de uma pirâmide é o segmento que parte do vértice até a base da lateral, formando um ângulo reto, isto é, a medida da altura da face lateral.
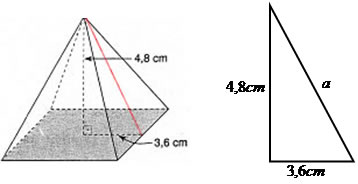
a² = 3,6² + 4,8²
a² = 12,96 + 23,04
a² = 36
√a² = √36
a = 6 cm
