Numeros Racionais e Numeros Inteiros

Pertencem ao conjunto dos naturais os números inteiros positivos incluindo o zero. Representado pela letra N maiúscula. Os elementos dos conjuntos devem estar sempre entre chaves.
N = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, ... }

- Quando for representar o Conjunto dos Naturais não – nulos (excluindo o zero) devemos colocar * ao lado do N.
Representado assim:
N* = {1, 2,3 ,4 ,5 ,6 ,7 ,8 ,9 ,10 ,11 ,12, ... }

A reticência indica que sempre é possível acrescentar mais um elemento.
N = {0, 1, 2, 3, 4, 5, 6, ...} ou N = {0, 1, 2, 3, 4, 5, 6, 7, ... }

Qualquer que seja o elemento de N, ele sempre tem um sucessor. Também falamos em antecessor de um número.
• 6 é o sucessor de 5.
• 7 é o sucessor de 6.
• 19 é antecessor de 20.
• 47 é o antecessor de 48.
Como todo número natural tem um sucessor, dizemos que o conjunto N é infinito.

Quando um conjunto é finito?
O conjunto dos números naturais maiores que 5 é infinito: {6, 7, 8, 9, ...}
Já o conjunto dos números naturais menores que 5 é finito: {0, 1, 2, 3, 4}
Veja mais alguns exemplos de conjuntos finitos.
• O conjunto dos alunos da classe.
• O conjunto dos professores da escola.
• O conjunto das pessoas que formam a população brasileira.

Interseção do conjunto dos naturais e dos inteiros.

Pertencem ao conjunto dos números inteiros os números negativos, os números positivos e o zero. Fazendo uma comparação entre os números naturais e os inteiros percebemos que o conjunto dos naturais está contido no conjunto dos inteiros.

N = { 0,1,2,3,4,5,6, ... }

Z = { ... , -3,-2,-1,0,1,2,3,4, ... }

N Z

O conjunto dos números inteiros é representado pela letra Z maiúscula. Os números positivos são representados com o sinal de (+) positivo na frente ou com sinal nenhum (+2 ou 2), já os números negativos são representados com o sinal de negativo (-) na sua frente (-2).

►Os números inteiros são encontrados com freqüência em nosso cotidiano, por exemplo:

♦ Exemplo 1: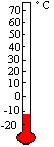

Um termômetro em certa cidade que marcou 10^°C acima de zero durante o dia, à noite e na manhã seguinte o termômetro passou a marcar 3°C abaixo de zero. Qual a relação dessas temperaturas com os números inteiros?

Quando falamos acima de zero, estamos nos referindo aos números positivos e quando falamos dos números abaixo de zero estamos referindo aos números negativos.

+10° C ------------- 10° C acima de zero
- 3° C --------------- 3° C abaixo de zero

♦ Exemplo 2:

Vamos imaginar agora que uma pessoa tem R$500,00 depositados num banco e faça sucessivas retiradas:

• dos R$500,00 retira R$200,00 e fica com R$300,00

• dos R$300,00 retira R$200,00 e fica com R$100,00

• dos R$100,00 retira R$200,00 e fica devendo R$ 100,00

A última retirada fez com que a pessoa ficasse devendo dinheiro ao banco. Assim:

Dever R$100,00 significa ter R$100,00 menos que zero. Essa dívida pode ser representada por – R$100,00.

►Oposto de um número inteiro

O oposto de um número positivo é um número negativo simétrico. Por exemplo: o oposto de +2 é -2; o oposto de -3 é +3.

►O conjunto dos números inteiros possui alguns subconjuntos:

- Inteiros não – nulos
São os números inteiros, menos o zero.
Na sua representação devemos colocar * ao lado do Z.
Z* = {..., -3, -2, -1, 1, 2, 3,...}

- Inteiros não positivos
São os números negativos incluindo o zero.
Na sua representação deve ser colocado - ao lado do Z.
Z_ = {..., -3, -2, -1, 0}

- Inteiros não positivos e não – nulos
São os números inteiros do conjunto do Z_ excluindo o zero.
Na sua representação devemos colocar o _ e o * ao lado do Z.
Z*_ = {..., -3, -2, -1}

- Inteiros não negativos
São os números positivos incluindo o zero.
Na sua representação devemos colocar o + ao lado do Z.
Z + = { 0,1 ,2 ,3, 4,...}
O Conjunto Z ₊ é igual ao Conjunto dos N

- Inteiros não negativos e não - nulos
São os números do conjunto Z+, excluindo o zero.
Na sua representação devemos colocar o + e o * ao lado do Z.
Z* + = {1, 2, 3, 4,...}
O Conjunto Z* ₊ é igual ao Conjunto N*

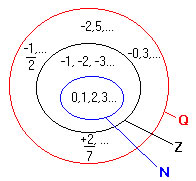
Interseção dos conjuntos: Naturais, Inteiros e Racionais.

Os números decimais são aqueles números que podem ser escritos na forma de fração.

Podemos escrevê-los de algumas formas diferentes:
Por exemplo:

♦ Em forma de fração ordinária: ; ; e todos os seus opostos.

Esses números tem a forma com a , b Z e b ≠ 0.

♦ Números decimais com finitas ordens decimais ou extensão finita:



Esses números têm a forma 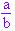com a , b 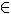Z e b ≠ 0.

♦ Número decimal com infinitas ordens decimais ou de extensão infinita periódica. São dízimas periódicas simples ou compostas:



As dízimas periódicas de expansão infinita, que podem ser escritas na forma : com a, b 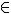Z e b ≠ 0.

► O conjunto dos números racionais é representado pela letra Q maiúscula.

Q = {x = , com a Z e b Z*}

►Outros subconjuntos de Q:

Além de N e Z, existem outros subconjuntos de Q.

Q^* ---------- É o conjunto dos números racionais diferentes de zero.

Q₊ ---------- É o conjunto dos números racionais positivos e o zero.

Q_- ----------- É o conjunto dos números racionais negativos e o zero.

Q_^*+ ---------- É o conjunto dos números racionais positivos.

Q^*_- ----------- É o conjunto dos números racionais negativos.


► Representação Geométrica

Entre dois números racionais existem infinitos outros números racionais.

Por Danielle de Miranda
Graduada em Matemática
Equipe Brasil Escola