Somatório: um conceito importante
Calcule o valor da soma S = 1.2 + 2.3 + 3.4 + 4.5 + 5.6 + 6.7 + ... + n.(n + 1) para n ³ 1.
Solução:
Na soma acima, observe que o termo de ordem n (n-ésimo termo ou enésimo termo) é igual a
n.(n + 1)
Seja Ti um termo qualquer da soma acima. Podemos escrever Ti = i.(i + 1) = i2 + i
Com efeito, por exemplo o 5º termo é igual a 5.6 ou seja, T5 = 5.(5+1) = 5.6
O sexto termo é igual a 6.7, ou seja T6 = 6.(6 + 1) = 6.7 e assim sucessivamente.
Para facilitar a resolução da questão, vamos usar a notação de somatório. Antes porém, vamos revisar a notação de somatório.
Seja a soma p1 + p2 + p3 + p4 + ... + pn . Observe que um termo qualquer desta soma poderia ser representado por pi onde i = 1, 2, 3, ... , n.
A notação de somatório permite simplificar a exibição da soma acima, utilizando como símbolo, a letra grega maiúscula sigma (S) da seguinte forma: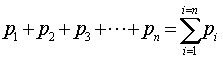
que lê-se: somatório de todos os pi com i variando de 1 a n.
De modo inverso, poderemos desenvolver um somatório. Veja o exemplo:
a)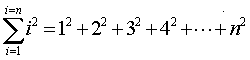
b)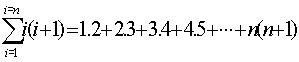
c)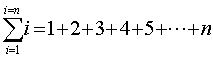
Uma propriedade importante dos somatórios é a seguinte: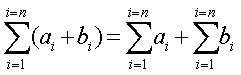
ou seja: o somatório de uma soma é igual à soma dos somatórios.
Usando a nova simbologia introduzida acima, poderemos escrever a soma
S = 1.2 + 2.3 + 3.4 + 4.5 + 5.6 + 6.7 + ... + n.(n + 1) para n ³ 1 ou,
S = 1.2 + 2.3 + 3.4 + 4.5 + 5.6 + 6.7 + ... + n2 + n para n ³ 1
na seguinte forma de somatório: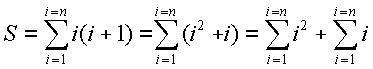
onde i = 1, 2, 3, ... , n, pois já vimos acima que sendo Ti um termo qualquer da soma que desejamos calcular, podemos escrever Ti = i.(i + 1) = i2 + i.
Então, a soma procurada S = 1.2 + 2.3 + 3.4 + 4.5 + 5.6 + 6.7 + ... + (n2 + n) pode ser decomposta na forma:
S = (12 + 22 + 32 + 42 + ... + n2 ) + (1 + 2 + 3 + 4 + ... + n)
Ora, o valor da primeira parcela 12 + 22 + 32 + 42 + ... + n2 , eu já calculei no arquivo Uma soma de quadrados (para retornar clique em VOLTAR no seu navegador) e é igual a:
12 + 22 + 32 + 42 + ... + n2 = [n(n+1)(2n+1)]/6
A segunda parcela 1 + 2 + 3 + 4 + ... + n é a soma dos n primeiros termos de uma PA (para retornar clique em VOLTAR no seu navegador) de primeiro termo 1 e último termo n,
cujo resultado é [(1 + n).n] / 2.
Substituindo, fica:
S = (12 + 22 + 32 + 42 + ... + n2 ) + (1 + 2 + 3 + 4 + ... + n) =
= [n(n+1)(2n+1)]/6 + [(1 + n).n] / 2
Efetuando as operações indicadas, vem:
[(n2 + n)(2n+1)] / 6 + (n + n2) / 2 = [(2n3 + n2 + 2n2 + n) / 6] + (n2 + n) / 2 =
= [(2n3 + n2 + 2n2 + n) / 6] + (3n2 + 3n) / 6 =
= [(2n3 + 6n2 + 4n) / 6
Dividindo tudo por 2, vem, finalmente:
S = (n3 + 3n2 + 2n) / 3
Portanto, chegamos à brilhante conclusão: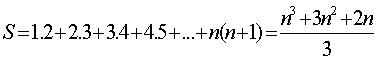
Assim, por exemplo, se n = 4 (tomando os quatro primeiros termos da soma), teríamos:
S = 1.2 + 2.3 + 3.4 + 4.5 = (43 + 3.42 + 2.4) / 3 = 120 / 3 = 40.
Assim, por exemplo, se n = 5 (tomando os cinco primeiros termos da soma), teríamos:
S = 1.2 + 2.3 + 3.4 + 4.5 + 5.6 = (53 + 3.52 + 2.5) / 3 = 210/3 = 70.
E assim sucessivamente.
Uma outra conclusão brilhante que podemos tirar do exercício acima é que, para todo n inteiro maior ou igual a 1, o trinômio n3 + 3n2 + 2n será sempre um número divisível por 3.
Isto nos leva a afirmar por exemplo que o número (gigantesco)
1000003 + 3.1000002 + 2.100000 é divisível por 3, entre outros infinitos exemplos que poderiam ser apresentados.