É papel do educador combater o medo de errar que inibe, as possibilidades de realização e satisfação. "Prof. Marcondes Diniz Martins"
sexta-feira, 30 de dezembro de 2011
terça-feira, 27 de dezembro de 2011
segunda-feira, 26 de dezembro de 2011
Numeração decimal IV
As figuras foram divididas em 10 e 100 pares, respectivamente. A seguir foram coloridas de verde escuro 4 e 40 destas parte, respectivamente. Observe:
Logo, decimais equivalentes são aqueles que representam a mesma quantidade.
Exemplos:
| 0,4 = 0,40 = 0,400 = 0,4000 | 8 = 8,0 = 8,00 = 8,000 |
| 2,5 = 2,50 = 2,500 = 2,5000 | 95,4 = 95,40 = 95,400 = 95,4000 |
| Um número não se altera quando se acrescenta ou se suprime um ou mais zeros à direita de sua parte decimal. |
Comparar dois números decimais significa estabelecer uma relação de igualdade ou de desigualdade entre eles. Consideremos dois casos:
1º Caso: As partes inteira
O maior é aquele que tem a maior parte inteira.
|
O maior é aquele que tem a maior parte decimal. É necessário igualar inicialmente o número de casas decimais acrescentando zeros.
|
- 0,75 > 0,7 ou 0,75 > 0,70 (igualando as casas decimais), pois 75 > 70.
- 8,3 > 8,03 ou 8,30 > 8,03 (igualando as casas decimais ), pois 30 > 3.
Numeração decimal
Numeração decimal
Transformação de números decimais em frações decimais
Observe os seguintes números decimais:
-
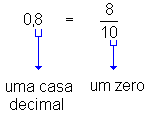
0,8 (lê-se "oito décimos"), ou seja,
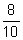 .
. -
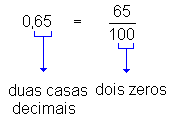
0,65 (lê-se "sessenta e cinco centésimos"), ou seja,
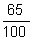 .
. -
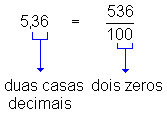
5,36 (lê-se "quinhentos e trinta e seis centésimos"), ou seja,
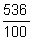 .
. -
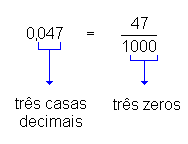
0,047 (lê-se "quarenta e sete milésimos"), ou seja,
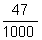
Verifique então que:
 |  |
 |  |
Assim:
| Um número decimal é igual à fração que se obtém escrevendo para numerador o número sem vírgula e dando para denominador a unidade seguida de tantos zeros quantas forem as casas decimais. |
Transformação de fração decimal em número decimal
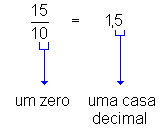
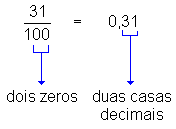
Observe as igualdades entre frações decimais e números decimais a seguir:
 |  |
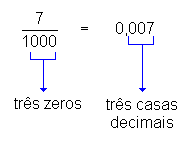 | 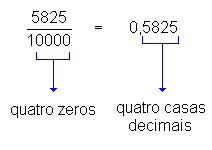 |
Podemos concluir, então, que:
Para se transformar uma fração decimal em número decimal, basta dar ao numerador tantas casas decimais quantos forem os zeros do denominador.fonte :http://www.somatematica.com.br
Numeração decimal III
Numeração decimal
Leitura dos números decimais
No sistema de numeração decimal, cada algarismo, da parte inteira ou decimal, ocupa uma posição ou ordem com as seguintes denominações:
| ||||||||||||||||||
Leitura
Lemos a parte inteira, seguida da parte decimal, acompanhada das palavras:
décimos ........................................... : quando houver uma casa decimal;
centésimos....................................... : quando houver duas casas decimais;
milésimos......................................... : quando houver três casas decimais;
décimos milésimos ........................ : quando houver quatro casas decimais;
centésimos milésimos ................... : quando houver cinco casas decimais e, assim sucessivamente.
Exemplos:
1,2: um inteiro e dois décimos;
2,34: dois inteiros e trinta e quatro centésimos
Quando a parte inteira do número decimal é zero, lemos apenas a parte decimal.
Exemplos:
0,1 : um décimo;
0,79 : setenta e nove centésimos
Observação:
1. Existem outras formas de efetuar a leitura de um número decimal. Observe a leitura do número 5,53:
Leitura convencional: cinco inteiros e cinquenta e três centésimos;
Outras formas: quinhentos e cinquenta e três centésimos;
cinco inteiros, cinco décimos e três centésimos.
2. Todo números natural pode ser escrito na forma decimal, bastando colocar a vírgula após o último algarismo e acrescentar zero(s). Exemplos:
4 = 4,0 = 4,00 75 = 75,0 = 75,00
fonte :http://www.somatematica.com.brNumeração decimal II
Numeração decimal
Números Decimais
O francês Viète (1540 - 1603) desenvolveu um método para escrever as frações decimais; no lugar de frações, Viète escreveria números com vírgula. Esse método, modernizado, é utilizado até hoje.
Observe no quando a representação de frações decimais através de números decimais:
| Fração Decimal | = | Números Decimais |
| = | 0,1 | |
| = | 0,01 | |
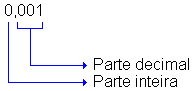
| = | 0,001 | |
| = | 0,0001 |
| Fração Decimal | = | Números Decimais |
| = | 0,5 | |
| = | 0,05 | |
| = | 0,005 | |
| = | 0,0005 |
| Fração Decimal | = | Números Decimais |
| = | 11,7 | |
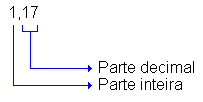
| = | 1,17 | |
| = | 0,117 | |
| = | 0,0117 |
Os números 0,1, 0,01, 0,001; 11,7, por exemplo, são números decimais.
Nessa representação, verificamos que a vírgula separa a parte inteira da parte decimal.
|
|
|
Numeração decimal
Numeração decimal
Introdução
A figura nos mostra um paralelepípedo com suas principais dimensões em centímetros.
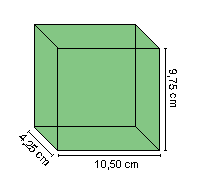
Essas dimensões são apresentadas sob a forma de notação decimal, que corresponde a uma outra forma de representação dos números racionais fracionários.
A representação dos números fracionária já era conhecida há quase 3.000 anos, enquanto a forma decimal surgiu no século XVI com o matemático francês François Viète.
O uso dos números decimais é bem superior ao dos números fracionários. Observe que nos computadores e nas máquinas calculadoras utilizamos unicamente a forma decimal.
Frações Decimais
Observe as frações:
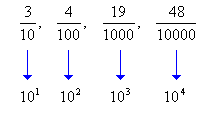
Os denominadores são potências de 10.
Assim:
Denominam-se frações decimais, todas as frações que apresentam potências de 10 no denominador.fonte :http://www.somatematica.com.br
terça-feira, 15 de novembro de 2011
Política
Por que o Estado de Minas Gerais não tem dinheiro para pagar o Piso Salarial
Fonte :http://blogdabeatrizcerqueira.blogspot.com/
domingo, 13 de novembro de 2011
Quem é esse usuário de drogas

O mercado de drogas segue a lógica capitalista de mercado e rende bilhões de dólares anualmente para os grandes cartéis mexicanos e colombianos gerando também assaltos, assassinatos e corrupções. Os lucros exorbitantes, livres de impostos e fiscalizações, são garantidos à custa de viciados nas mais variadas drogas em todo mundo. O tráfico de drogas é uma rede global de pequenas redes locais, assim como o crime organizado que tem nas drogas uma das suas diversas fontes de renda. E quem é o usuário que alimenta toda essa rede?
O consumo de drogas ilícitas é uma realidade independente de classe social, nível intelectual, nacionalidade ou idade. Para o usuário miserável que vive nas ruas, existe a pedra de crack, para o jovem de classe média existe a opção, além da terrível pedra de crack, dos papelotes de cocaína e das buchas de maconha, e para os mais abastados todas as opções anteriores somadas às drogas sintéticas (Extasy) tão curtidas nas badaladas boates e festas RAVE.
Mas, quem é esse usuário que além de causar tantos danos à sociedade destrói a sua própria família? Além de sustentar redes nacionais e internacionais de tráfico de drogas, financiar o tráfico de armas e o suborno de autoridades, garantir receitas milionárias aos grandes traficantes que matam, extorquem, apavoram comunidades inteiras e espalham o medo, esses usuários causam danos, as vezes inversíveis no seio de suas famílias. Roubam os pais, vendem os eletrodomésticos, agridem os avós para se apoderarem mensalmente das pensões, provocam o assassinato de membros de sua família por traficantes cobrando dívidas e por fim, tais usuários, viram clientes das batidas policiais e do sistema prisional.
A tendência mundial no trato com as drogas é o tratamento do dependente químico e a não criminalização do usuário, permanecendo a criminalização do traficante. Ou seja, que o usuário seja tratado pela saúde pública e não pela segurança pública. O combate repressivo ao tráfico, tendência liderada pelos Estados Unidos, tem provado a cada relatório da ONU, que está sendo ineficiente na redução da oferta de drogas. Essa ineficiência na redução da oferta não está relacionada aos bilhões de dólares e movimentação de exércitos para confronto e destruição de plantações de coca, ópio e laboratórios, e sim ao aumento da demanda de usuários. Enfim, é o usuário que determina o custo da destruição e das perdas humanas e sociais.
Depois de financiar os prejuízos sociais, em níveis globais locais, e de sua própria família, esse usuário paga pela sua própria decadência moral, física, emocional e social quando se mantém na condição de viciado, de dependente químico. Portanto, espera-se do Poder Público algo mais além dos simples planos emergências de combate às drogas. O uso das drogas, assim com a violência por ela causada, é um problema real e imenso o bastante para não ser enfrentado somente por políticas públicas de urgência que dispensa milhões de reais do dinheiro público sem que se alcance o retorno desejado que é ao menos o controle.
Fonte : http://nepfhe-educacaoeviolencia.blogspot.com/2010/07/quem-e-esse-usuario-de-drogas.html
domingo, 16 de outubro de 2011
O Grau
1. O Grau
Definimos como 1 grau o arco equivalente a  a circunferência, isto é, em uma circunferência cabem 360 º.
a circunferência, isto é, em uma circunferência cabem 360 º.
Exemplos:
Dividindo a circunferência em 4, 6 e 8 partes congruentes, temos:

O grau comporta ainda os submúltiplos, minuto(,) e segundo(,,), de forma que:
1º =60' e 1'`=60,,
O Radiano
Definimos 1 radiano como o arco cujo comprimento é igual ao raio da circunferência onde tal arco foi determinado.

A partir da figura, imagine que o arcos AB foi retificado. O Segmento AB obtido, tendo comprimento igual ao raio da circunferência, indica que a medida do arco, em radianos, equivale ao número de vezes que o comprimento do raio cabe nesse arco, ou seja, sendo 1 e R os comprimentos do arco e do raio da circunferência, respectivamente, temos:
a=1/R
Lembramos que o comprimento de uma circunferência de raio R é dado por 2pR. Utilizando a relação apresentada acima, para calcularmos em radianos a medida a de um arco de uma volta, fazemos:
alfa=2pR/R = 2prad
Exemplos:



Fonte : http://educar.sc.usp.br/licenciatura/1999/ARCOS.HTML
Conceituando o Ciclo Trigonométrico
1. Conceituando o Ciclo Trigonométrico
As razões trigonométricas, aplicadas a arcos de uma circunferência, mantêm as mesmas propriedades que demonstramos ser válidas quando utilizadas com ângulos agudos.
Inicialmente, deveremos definir uma circunferência, em especial, sobre a qual interpretaremos as nossas já conhecidas razões trigonométricas.
Tal circunferência recebe o nome de circunferência trigonométrica ou ciclo trigonométrico.
Imaginemos, primeiramente, um sistema de coordenadas cartesianas, como indicado na figura 1.

(figura 1)
Nos eixos r e s, perpendiculares entre si, cada ponto corresponde a um número real e vice-versa: cada número real tem um ponto associado em cada uma das retas. À interseção dos eixos faremos corresponder o número zero, tanto para o eixo r, das abscissas, como para o eixo s, das ordenadas, constituindo o que chamamos de origem dos eixos coordenados.
Assim, qualquer ponto do plano determinado pode ser representado por um par de números reais, a que chamamos de par ordenado. O ponto P, na figura, terá então as coordenadas (a, b), sendo a a abscissa de P e b a sua ordenada.
Na figura 2, fazemos surgir o ciclo trigonométrico, com centro na origem dos eixos e raio unitário.

(figura 2)
Como consequência, os pontos de interseção da circunferência com o par de eixos, indicados na figura por A, B, C e D, terão coordenadas dadas respectivamente por (1, 0), (0, 1), (_ 1, 0) e (0, _ 1).
Esses pontos dividem o ciclo trigonométrico em quatro arcos congruentes, aos quais damos o nome de quadrantes, numerados a partir de A no sentido anti-horário.
Por convenção, A, B, C e D são apenas limitadores dos quadrantes, não pertencendo a nenhum deles. Por exemplo, D é ponto que separa 3º do 4º quadrantes, mas não lhes pertence.
2. Números Reais no Ciclo Trigonométrico
Vamos associar a cada número real x um ponto do ciclo trigonométrico, de tal forma que:
_ o ponto A esteja associado ao número x = 0;
_ um número real x seja associado a um ponto P, tal que o comprimento do arco seja igual a | x |;
_ se x > 0, o arco será determinado, sobre o ciclo, no sentido anti-horário; se x < 0, o arco será
definido no sentido horário, como indicamos na figura 3.

(figura 3)
O ponto P, determinado de acordo com o que apresentamos acima, associado a um número real x, é denominado de imagem de x no ciclo trigonométrico.
Lembremos que o comprimento da circunferência trigonométrica pode ser calculado por C = 2R, sendo R o seu raio.
Como ele tem por medida uma unidade, o comprimento do ciclo trigonométrico será igual, portanto, a 2 unidades. Como decorrência, temos que:
_ um arco de uma volta (ou de medida 2 rad) terá comprimento 2 unidades;
_ um arco de comprimento |x|, no ciclo trigonométrico, terá medida |x| rad.
Assim, a medida de um arco , sobre o ciclo trigonométrico, é igual ao módulo do número real x do qual P é a imagem.
Fonte: http://educar.sc.usp.br/licenciatura/1999/CICLO.HTML
Círculo Trigonométrico
Movimente o ponto verde e observe as alterações do eixos do seno, cosseno e tangente.
http://www.geogebra.org/en/upload/files/Brasil/Orestes/circtrig.html
sábado, 24 de setembro de 2011
INTRIGANTE DE FATO!
É um mistério; ou não!
1/1/11, 1/11/11, 11/1/11, 11/11/11 e Tem mais!!!
Pegue os últimos 2 dígitos do ano em que você nasceu mais a
idade que você vai ter este ano e a sua soma será igual a
111 para todos! Por exemplo: o Roberto nasceu em 1981 e vai fazer 30 anos. Portanto: 81 + 30 = 111
terça-feira, 16 de agosto de 2011
Produtos Notáveis (E M)
Cubo da soma de n termos

sendo que i
Diferença entre os quadrados da soma e diferença
(a+b)² - (a-b)² = 4ab
Exemplo: (7+9)²-(7-9)²=4×7×9
Soma dos quadrados da soma e da diferença
(a+b)² + (a-b)² = 2(a²+b²)
Exemplo: (3+5)²+(3-5)²=2(3²+5²)
Soma de dois cubos
a³+b³ = (a+b)³ - 3ab(a+b)
Exemplo: 2³+4³=(2+4)³-3×2×4×(2+4)
Soma de dois cubos na forma fatorada
a³+b³ = (a+b)(a²-ab+b²)
Exemplo: 5³+7³=(5+7) (5²-5×7+7²)
Transformação do produto na diferença de quadrados
ab = [½(a+b)]² - [½(a-b)]²
Exemplo: 3×5=[½(3+5)]²-[½(3-5)]²
Diferença de potências (ordem 4)
a4-b4 = (a-b)(a+b)(a²+b²)
Exemplo: 54-14=(5-1)(5+1)(5²+1²)
Diferença de potências (ordem 6)
a6-b6 = (a-b)(a+b)(a²+ab+b²)(a²-ab+b²)
Exemplo: 56-16=(5-1)(5+1) (5²+5×1+1²)(5²-5×1+1²)
Diferença de potências (ordem 8)
a8 - b8 = (a-b)(a+b)(a²+b²)(a4+b4)
Exemplo: 58-18=(5-1)(5+1)(5²+1²)(54+14)
Produto de três diferenças
(a-b)(a-c)(b-c) = ab(a-c) + bc(b-c) + ca(c-a)
Exemplo: (1-3)(1-5)(3-5)=1×3×(1-5)+3×5×(3-5)+5×1×(5-1)
Produto de três somas
(a+b)(b+c)(c+a) = (a+b+c)(ab+bc+ac) - abc
Exemplo: (1+3)(3+5)(5+1)=(1+3+5)(1×3+3×5+1×5)-1×3×5
Soma de cubos das diferenças de três termos
(a-b)³ + (b-c)³ + (c-a)³ = 3(a-b)(b-c)(c-a)
Exemplo: (1-3)³+(3-5)³+(5-1)³=3(1-3)(3-5)(5-1)
Cubo da soma de três termos
(a+b+c)³ = (a+b-c)³ + (b+c-a)³ + (a+c-b)³ + 24abc
Exemplo: (7+8+9)³=(7+8-9)³+(8+9-7)³+(7+9-8)³+24×7×8×9
Soma nula de produtos de cubos por diferenças
a³(b-c)+b³(c-a)+c³(a-b)+(a+b+c)(a-b)(b-c)(a-c)=0
Exemplo: 2³(4-6)+4³(6-2)+6³(2-4)+(2+4+6)(2-4)(4-6)(2-6)=0
Soma de produtos de cubos com diferenças
a³(b-c)³ + b³(c-a)³ + c³(a-b)³ = 3abc(a-b)(b-c)(a-c)
Exemplo: 7³(8-9)³+8³(9-7)³+9³(7-8)³=3.7.8.9(7-8)(8-9)(7-9)
Produto de dois fatores homogêneos de grau dois
(a²+ab+b²) (a²-ab+b²)=a4+a² b²+b4
Exemplo: (5²+5×7+7²)(5²-5×7+7²)=54+5² 7²+74
Soma de quadrados de somas de dois termos
(a+b)²+(b+c)²+(a+c)²=(a+b+c)²+a²+b²+c²
Exemplo: (1+3)²+(3+5)²+(1+5)²=(1+3+5)²+1²+3²+5²
Produto de quadrados de fatores especiais
(a-b)² (a+b)² (a²+b²)²=(a4-b4)²
Exemplo: (7-3)² (7+3)² (7²+3²)²=(74-34)²
Soma de quadrados de express. homogêneas de grau 1
(a+b+c)²+(a-b)²+(b-c)²+(c-a)²=3(a²+b²+c²)
Exemplo:
(7+8+9)²+(7-8)²+(8-9)²+(9-7)²=3(7²+8²+9²)
Identidade de interpolação

Exemplo: Com a=1, b=2 e c=3 na identidade, obtemos:

Fonte: pessoal.sercomtel.com.br
sexta-feira, 5 de agosto de 2011
Derivadas de funções exponencial e logarítmica
Derivada do logaritmo natural
![]()
Derivada do logaritmo em outras bases
![]()
Exponencial
![]()
![]()
![]()
Lembre-se da definição da função logarítmica com base a > 0:
Fonte : http://www.somatematica.com.br/superior/derivada.php