Letra Q
QUADRADO - Um quadrilátero que tem todos os quatro ângulos retos e os quatro lados congruentes, paralelos dois a dois.
QUADRADO MÁGICO - Os números são dispostos em quadrados (3 x 3, 4 x 4, 5 x 5, ...) de modo que a soma dos números na vertical, na horizontal ou na diagonal é sempre a mesma.
QUADRADO PERFEITO - São os números que tem uma raiz quadrada inteira.
QUADRANTE - Uma região do plano cartesiano delimitada por duas semi-retas. O plano cartesiano possui 4 quadrantes.
QUADRICELULAR - que é dividido em células.
QUADRÍDUO - Espaço de quatro dias.
QUADRIÊNIO - Período de quatro anos.
QUADRILÁTERO - Um polígono com quatro lados.
QUÁDRUPLO - Multiplicado por quatro; quatro vezes maior.
QUARTETO - Trecho de música executado por quatro vozes ou por quatro instrumentos.
QUARTILHO - A quarta parte de uma camada.
QÜINDÊNIO - Período de quinze anos.
QUINÁRIO - Aplica-se esse adjetivo ao elemento que contém cinco partes. Exemplo: Compasso quinário.
QUINGENTÉSIMO - Ordinal correspondente ao Cardinal 500.
QUINHENTISMO - Relativo ao século XVI que vai de 1501 até 1600. Os escritores desse século são chamados quinhentistas.
QUINQUAGÉSIMO - Ordinal correspondente ao cardinal 50.
QÜINQÜENAL - Que dura cinco anos, ou que ocorre de cinco em cinco anos.
QÜINQÜENÁRIO - Que dura cinco anos, ou que ocorre de cinco em cinco anos.
QÜINQÜÊNIO - Período de cinco anos.
QÜINQÜÍDIO - Espaço de cinco dias.
QUINTETO - Composição musical de cinco instrumentos.
QUINTILHA - Estância de cinco versos.
QUINZENA - Período de quinze dias sucessivos. Uma das partes do mês dividido em duas partes iguais.
QUOCIENTE - O resultado de uma divisão. Na divisão de 8 por 4 o quociente é 2.
Letra R
RACIONALIZAR UMA FRAÇÃO - Obter uma fração equivalente à dada, onde o denominador seja um número racional. Exemplo:
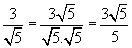
RADIANO - Unidade de medida de ângulo que corresponde ao ângulo central subtendido por um arco de circunferência cujo comprimento seja igual ao raio desta mesma circunferência.
RAIO - O segmento de reta que liga o centro do círculo a qualquer ponto da circunferência do círculo.
RAIZ DE UMA FUNÇÃO - Valor de x para o qual f(x) = 0.
RAIZ QUADRADA - A raiz quadrada de um número N é um número a tal que a x a = N. De uma maneira geométrica podemos dizer que a raiz quadrada de N é o lado quadrado cuja área é N. A raiz quadrada de 16 é 4 pois 4 x 4 = 16.
RAZÃO (:) - Comparação de dois números ou duas quantidades obtida pelo quociente entre elas. A razão entre 6 e 3 é igual a 2 a razão entre 3 e 6 é igual 0.5.
O termo razão também pode significar a diferença entre termos consecutivos de uma progressão aritmética, ou o quociente entre dois termos consecutivos de uma progressão geométrica.
REAJUSTE - Ajuste que se faz no preço das tarifas.
RECÍPROCO DE UM NÚMERO - Dois números são recíprocos se o seu produto é igual a 1. Também chamado inverso.
REDE - Obtém um padrão quando se desenvolve um sólido, isto é, se estende a superfície exterior de um sólido para obter uma superfície plana.
REDUÇÃO (Sistemas) - Método de resolução de um sistema que consiste em obter para uma das incógnitas, coeficientes com o mesmo valor. Assim ao somar algebricamente 2 a 2 essas equações faz-se desaparecer essa incógnita.
REFLEXÃO - A formação dos pontos de um objeto de modo que a nova figura obtida se pareça como uma imagem refletida em um espelho.
REGRESSÃO LINEAR - Método para encontrar a reta que mais se aproxima de um conjunto de pontos.
RELAÇÃO DE EULER (lê-se:"Óiler") - Em um poliedro convexo, a soma do número V de vértices com o número F de faces é igual ao número A de arestas mais dois.
V + F = A + 2
RENDA PER CAPTA - Quantia representativa da renda de cada pessoa de um país.
RESTO - A quantidade que sobra após a divisão de um número inteiro por outro. Ao dividir 13 por 4, o quociente é 3 e o resto é 1.
RETA - (Conceito primitivo) É um conjunto infinito de pontos alinhados de tal forma que os segmentos com extremidades em dois quaisquer desses pontos têm sempre a mesma inclinação.
RETÂNGULO - Paralelogramo que possui todos os ângulos retos e lados iguais dois a dois.
RETÂNGULO DE OURO - Trata-se de um retângulo construído de forma que o quociente entre os lados seja igual ao número de ouro.
RETA NUMERADA - Uma reta graduada que tem o número 0 (zero) como ponto inicial, um número 1 (unidade) como ponto de referência e outros números em ordem crescente (por convenção: para a direita), relativamente à medida do segmento que começa em 0 e termina em 1.
RETÂNGULO - Um paralelogramo que tem 4 ângulos retos e os lados são paralelos e congruentes dois a dois.
RETAS CONCORRENTES - Retas que se cruzam.
RETAS OBLÍQUAS - Duas retas que se cortam com um ângulo não perpendicular.
RETAS PARALELAS - Retas que nunca se cruzam e que não estão sobrepostas.
RETAS PERPENDICULARES - Retas que se cruzam formando um ângulo reto.
REVOLUÇÃO - Um deslocamento no qual cada ponto do objeto se desloca mantendo a mesma distância ao centro de rotação mas formando ângulos diferentes. Por exemplo, o movimento da roda de uma bicicleta é um movimento de rotação em torno de um eixo.
ROTAÇÃO - Um deslocamento no qual cada ponto do objeto se desloca mantendo a mesma distância ao centro de rotação mas formando ângulos diferentes. Por exemplo, o movimento da roda de uma bicicleta é um movimento de rotação em torno de um eixo.
Letra S
SECÇÕES CÔNICAS - Curvas que se obtém interseccionando uma superfície cônica por um plano. Conforme a posição do plano assim se obtém: ponto, circunferência, elipse, parábola, hipérbole.
SEGMENTO DE RETA - Parte de uma reta limitada entre dois pontos.
SEGUNDOS - Unidade de tempo traduzida por segundos = 1 minuto. Também chamamos segundos unidade de ângulos.
SEMANA - Espaço de sete dias. A palavra semana deriva-se de septum (sete) e mane (manhã ou dia).
SEMELHANTE - Diz-se que duas figuras são semelhantes se ambas são congruentes ou uma delas é uma ampliação ou redução da outra.
SEMICÍRCULO - Metade de um círculo, ou seja uma das partes do círculo delimitadas pelo diâmetro.
SENO (Sen) - Em um triângulo retângulo o sen A (ângulo agudo) é quociente entre o cateto oposto a esse ângulo e a hipotenusa.
SENTENÇA DE UMA FUNÇÃO - sua definição expressa através de variáveis. Ex: f(x) = 3x + 5.
SEPTULO - Que vale sete vezes outro, ou que é sete vezes maior que outro.
SEPTUPLICAR - Tornar sete vezes maior. Multiplicar por sete.
SEPTENATO - Denominação pela qual ficou conhecido o governo da França, estabelecido em 1873 e com a duração de sete anos.
SEQÜÊNCIA - Números ou figuras geométricas dispostos em certa ordem. 1, 3, 5, 7, ... é a seqüência dos números ímpares, por exemplo.
SETEMBRO - No calendário romano era setembro o sétimo mês do ano. No calendário muçulmano o sétimo mês correspondente ao Ramadã, isto é, o mês da quaresma.
SEXAGESIMAL - Unidade que utiliza a base 60. Como no caso da medida de ângulos onde um grau tem 60 minutos e um minuto tem 60 segundos.
SÍMBOLO - Sinal gráfico que representa uma idéia matemática. Os números são escritos com símbolos chamados ALGARISMOS.
SIMÉTRICO - Uma figura em uma, duas ou três dimensões é dita simétrica se ela possui um ente de simetria (ponto, eixo ou plano), de modo que do outro lado deste ente de simetria a figura seja semelhante, porém invertida, como se tivesse sido colocada na frente de um espelho.
SINAIS - Há diversos sinais que são usados na escrita matemática, como, por exemplo, os sinais das operações e os próprios algarismos. Para comparar números são usados os sinais: > (maior que), < (menor que), 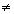 (diferente que), = (igual a)
(diferente que), = (igual a)
SISTEMA BINÁRIO - É um sistema de numeração que utiliza dois algarismos (0 e 1) para representar quantidades. Este é o sistema utilizado pelos computadores, pois precisamos de dois dígitos para representar as duas situações (ligado ou desligado) que ocorrem nos seus circuitos eletrônicos internos.
SISTEMA DECIMAL - É um sistema de numeração que utiliza dez algarismos para representar quantidades. Ex.: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
SISTEMA HEXADECIMAL - É um sistema de numeração que utiliza dezesseis algarismos para representar quantidades. Ex.: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F. Normalmente é vinculado à informática, pois os computadores interpretam as linguagens de programação em bytes, que são compostos de oito dígitos.
SISTEMA OCTAL - É um sistema de numeração que utiliza oito algarismos para representar quantidades. Ex.: 0, 1, 2, 3, 4, 5, 6, 7. É um sistema do tempo dos processadores de 8 bits. Atualmente este tipo de notação praticamente não é usado.
SISTEMA DE EQUAÇÕES - Conjunto de equações com as mesmas variáveis e que admitem as mesmas raízes.
SÓLIDO - Uma figura em três dimensões. Exemplos de sólidos são: cubo, paralelepípedo, pirâmide.
SOMA - Uma das principais operações básicas da aritmética, que resulta na adição de números.
SOMATÓRIO - Forma sintética de indicar uma adição de parcelas diferentes. O símbolo usado é um sigma maiúsculo. Exemplo: 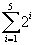 esta nomenclatura é o mesmo que escrever a soma de potências de 2 cujos expoentes vão de 1 a 5, ou seja 2 + 4 + 8 + 16 + 32.
esta nomenclatura é o mesmo que escrever a soma de potências de 2 cujos expoentes vão de 1 a 5, ou seja 2 + 4 + 8 + 16 + 32.
SUBCONJUNTO - Diz-se que A é um subconjunto de B se todos os elementos de A pertencem a B.
SUBSTITUIÇÃO - Método de resolução de um sistema de equações que consiste em determinar em uma delas o valor de uma incógnita e substituir nas restantes equações, essa incógnita pelo valor encontrado.
SUBTRAÇÃO - Uma das quatro operações básicas da aritmética, que objetiva retirar um número de outro. É uma operação artificial criada a partir da adição.
SUCESSÃO - Conjunto de objetos apresentados segundo uma certa sequência. Exemplo: Qual o número seguinte das sucessões: 1, 2, 3, 4.... e 7, 14, 21, 28, 35... São respectivamente 5 e 42.
SUCESSÃO DE FIBONACCI - Uma sucessão infinita onde cada termo é obtido pela adição dos dois anteriores. Na natureza ela aparece com frequência, por exemplo na distribuição das "pétalas" de uma pinha. Exemplo: 1, 1, 2, 3, 5, 8, 13, 21 ...
SUPERFÍCIE - Um ente geométrico bidimensional suave (que não possui bicos) e que possui medida de área, isto é, uma região que pode ser planificada (colocada sobre um plano) de modo que a nova região planificada tenha a área equivalente a de um quadrado.
SUPERFÍCIE CILÍNDRICA - Superfície gerada por uma reta (geratriz) que se desloca paralelamente a si mesma e apoiada numa curva (diretriz).
SUPERFÍCIE CÔNICA - Superfície gerada por uma reta (geratriz) que se desloca apoiada em uma curva (diretriz) mantendo um ponto fixo (vértice).
Letra T
TABUADA - Tabela usada nas séries iniciais que contém as operações aritméticas fundamentais.
TANGENTE - Linha ou superfície que toca outra linha ou superfície em um só ponto sem haver intersecções.
TANGRAM - Conjunto de peças gráficas específicas que pode ser reunido para montar figuras geométricas. Muito utilizado nas atividades práticas de Geometria.
TENTATIVA E ERRO, CHUTE - Uma estratégia de resolução de problemas onde se faz uma escolha para viabilizar o resultado. Assim, procede-se várias vezes até que se chegue a alguma conclusão próxima ao objetivo para a resolução do problema.
TEODOLITO - Instrumento óptico para medir com precisão ângulos horizontais e ângulos verticais; muito usado em trabalhos topográficos e geodésicos.
TEOREMA - Proposição que, para se tornar evidente, precisa de demonstração.
TERMO - Um dos objetos matemáticos em uma operação.
TETRAEDRO - Um poliedro com 4 faces. Se o tetraedro for regular, ele terá 4 faces congruentes, 4 vértices e 6 arestas também congruentes.
TONELADA - (t) Medida de massa em que 1 tonelada = 1000 quilogramas.
TOTAL - O resultado de uma adição, subtração, multiplicação, divisão.
TRANFERIDOR - Um instrumento que serve para medir ângulos.
TRANSITIVA - Nas igualdades: se a = b e b = c, então a = c. Nas desigualdade: se a > b e b > c, então a > c ou se a <>
TRANSLAÇÃO - Movimentar uma figura por forma que todos os seus pontos se desloquem na mesma direção e sentido mantendo as distâncias entre eles. Transformação geométrica que respeita as características já apontadas.
TRAPEZÓIDE - que tem a forma de um trapézio; trapezoidal.
TRIGONOMETRIA - Ramo da matemática que estuda no triângulo as relações entre as medidas dos lados e amplitude dos ângulos.
TRIÂNGULO - Polígono de três lados.
TRIÂNGULO ACUTÂNGULO - todos os ângulos internos são agudos, isto é, as medidas dos ângulos são menores do que 90º.
TRIÂNGULO DE PASCAL - Uma forma de dispor números (na forma de triângulo) em que o elemento inicial e o final de cada linha são 1, e os outros elementos obtém-se somando o elemento que o precede e o que lhe sucede na linha anterior.

TRIÂNGULO EQUILÁTERO - Os três lados têm medidas iguais (veja animação abaixo).
TRIÂNGULO ESCALENO - Os três lados têm medidas diferentes (veja animação abaixo).
TRIÂNGULO ISÓSCELES - Dois lados têm a mesma medida (veja animação abaixo).
TRIÂNGULO OBTUSÂNGULO - Um ângulo interno é obtuso, isto é, possui um ângulo com medida maior do que 90°.
TRIÂNGULO RETÂNGULO - Possui um ângulo interno reto (90 graus).
TRINÔMIO - Polinômio com três termos, três monômios.
Letras U/V
UNIÃO - Conjunto de todos os elementos pertencentes a dois ou mais conjuntos. Chama-se também reunião.
UNIDADE - A grandeza que serve de referência na medida. No caso da numeração o 1 é a unidade usada.
UNITÁRIO - Conjunto que tem um único elemento.
UNÍVOCA - Correspondência que faz com que um objeto corresponda a uma e somente uma imagem.
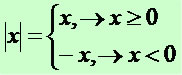
VALOR ABSOLUTO - O valor absoluto de um número real a, também chamado "módulo de a", é denotado por |a| e definido como o máximo valor entre a e -a, isto é:
|a| = max{a,-a}
VALOR POSICIONAL - O valor da posição de um algarismo depende de sua posição no número. No número 728, o algarismo 7 ocupa a posição das centenas, o 2 ocupa a posição das dezenas e o 8 a posição das unidades.
VARA - Medida antiga de comprimento equivalente a 1,10 m.
VARIÁVEL - A grandeza que pode ser mudada, ou melhor, cujo valor pode assumir diferentes grandezas. As letras mais usadas neste caso são as últimas letras do alfabeto: x, y e z, mas como mero hábito, já que a variável pode ser representada por qualquer símbolo. Exemplo: na equação f + 5 = 12, f é a variável ou incógnita, cujo valor determinado será 7.
VAZIO - Nome dado ao conjunto que não tem elementos. Representa-se por { } .
VELOCIDADE - Distância percorrida na unidade de tempo. Em um movimento uniforme pode-se calcular pela fórmula v = d / t.
VERTICAL - Reta perpendicular à horizontal. De outra maneira: reta na direção da força da gravidade (dirigida ao centro da terra).
VÉRTICE - O ponto de junção de duas semi-retas de um ângulo, de dois lados de um polígono ou de três (ou mais) faces de um sólido.
VETOR - Segmento de reta orientado, usado para a representação de forças, acelerações etc. Nessa representação aparece a grandeza (expressa pelo comprimento do segmento), a direção (dada pela reta) e o sentido (dado pela seta).
VETOR NULO - Vetor nulo ou vetor zero de um espaço vetorial.
VÍRGULA - É um sinal matemático que separa a parte inteira da parte decimal de um número.
VISTAS - Você pode olhar um objeto sob vários ângulos. Conforme o ângulo, você tem uma vista diferente desse objeto. Se você está em um avião sobrevoando uma cidade, você tem a vista superior da cidade. O mapa de uma cidade é a vista superior simplificada da cidade. A planta de uma casa também é a vista superior simplificada da casa.
VOLUME - O volume de um objeto é definido como a medida do lugar ocupado pelo objeto no espaço. Por exemplo, o volume de uma caixa é medido em cm³.
Letras X/Z
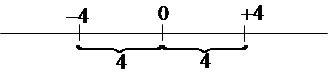
ZERO - Representação do nada. O mais recente dos algarismos. O ponto de separação dos números negativos e positivos na reta real.
ZERO DE UMA FUNÇÃO - Valor de x para o qual se tem f(x) = 0.