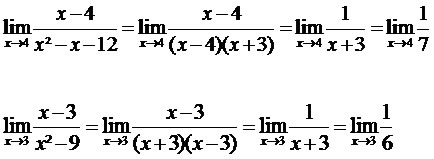É comum ouvirmos as seguintes frases: “Eu peso 85 kg”, “Estou acima do meu peso”, “O peso ideal para sua altura é 75 kg”. Popularmente, estamos associando a medida observada ao subirmos em uma balança à palavra peso. Essa argumentação utilizada por grande parte das pessoas está totalmente equivocada, pois não podemos relacionar peso com a massa de um corpo, que é a grandeza verificada na balança. As definições corretas são:
Peso é uma força “invisível” que atrai os corpos para a superfície da terra. Dessa forma, o nosso peso varia de acordo com o valor da gravidade, diferente em outros planetas e satélites naturais do sistema solar.
Massa é a quantidade de matéria presente em um corpo. Dizemos que a massa de uma pessoa é a mesma em qualquer lugar.
Por exemplo, vamos imaginar que uma pessoa tenha massa de 60 kg. De acordo com essa medida, podemos dizer que ela possui peso igual a aproximadamente 588 N (Newton). Vamos
entender o valor desse peso:
Quando nos referimos ao peso, dizendo que seu valor depende da gravidade, então estamos colocando em prática a 2ª
lei de Newton, demonstrada pela fórmula matemática: P = m * g. Nessa expressão, temos que:
P: peso
m: massa
g: aceleração da gravidadeContinuando com mais um exemplo, vamos determinar o peso de uma pessoa com massa igual a 57 kg, na terra, na lua e em outros planetas. Mas para isso, precisamos conhecer as acelerações da gravidade que estão presentes na tabela a seguir:

Uma pessoa com a massa igual a 57 kg possui os seguintes pesos:
Na terra
P = m * g → P = 57 * 9,8 → P = 558,6 N
Na lua
P = m * g → P = 57 * 1,67 → P = 95,19 N
Em Júpiter
P = 57 * 22,9 → P = 1 305,3 N
Em Plutão
P = 57 * 0,5 → P = 28,5 N
No sol
P = 57 * 274 → P = 15 618 N
Fonte : http://www.brasilescola.com