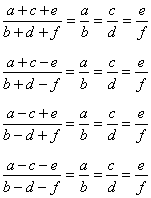Matemático e astrônomo polonês, autor da Teoria Heliocêntrica, segundo a qual o sol é o verdadeiro centro do sol é o verdadeiro centro do sistema solar, devendo-se a sucessão de dias e noites, ao movimento da rotação da Terra sobre seu próprio eixo. Copérnico nasceu em Tourun, na Posnâmia (região polonesa as margens do Vístula) na fronteira com a Alemanha, à 19/02/1453, era filho de um comerciante que o deixou órfão, aos 10 anos. Sua tutela ficou à cargo de seu tio Lucius Waczenrade, Bispo de Erimland. E ele cresceu em meio ao período Renascentista, no qual o saber, bem como a cultura avançaram revulucionariamente. Também serviu a Igreja Católica, o que de certa forma foi positivo, pois lhe dava acesso ao saber entesourado da igreja .
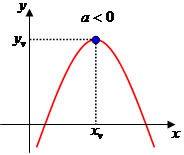
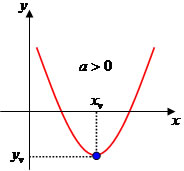
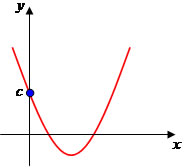
Propriedades planetárias
Em 1491, ingressou na Universidade de Cracóvia, onde estudou, principalmente, matemática. Depois na Universidade de Bolonha estudou grego e em Pádua Medicina. Em 1500 voltou a Polônia, e já como monge, assumiu as funções de cônego em Frauenburg, exercendo a medicina. Como sua verdadeira paixão era a astronomia, teve sua atenção despertada pelo planeta Marte, e de suas observações, veio-lhe as perguntas: - Por que os planetas se tornavam cada vez maiores, mais brilhantes, ao longo de sua trajetória? - Ou cresciam, o que parecia absurdo? - Ou ficavam tão mais perto da Terra? O que certamente, os levava a sair dos epiciclos, onde deveriam permanecer... Diante de suas dúvidas, Copérnico, com sua tranquilidade característica, passou a estudar os pensadores antigos, que ousaram dar um movimento à Terra, e colocar o Sol como centro do Universo. Depois de minuciosos cálculos matemáticos, ele deduziu: A Terra executa um movimento completo em torno de seu eixo. Isso explicaria o movimento do Sol e das Estrelas, produzindo o dia e a noite. Novos cálculos o levaram a atribuir ao Sol o movimento anual, que na verdade é executado pela Terra.
Suas afirmações eram contrárias a Teoria Geocêntrica, que afirmava ser a Terra fixa, e que todos os demais astros, giravam em torno dela. A igreja fundamentava-se na Teoria Geocêntrica, e agia de modo bravio, contra qualquer conceito contrário a esta teoria. A Teoria Geocêntrica, também chamada de Teoria Ptolemaica , por ter sido elaborada por Cláudio Ptolomeu, astrônomo e geógrafo grego do séc. II, dizia que a Terra era imóvel e ao seu redor giravam a Lua, o Sol, os Planetas e as Estrelas. Durante 30 anos, Copérnico, analisando e meditando suas próprias observações, concluiu sua Teoria. Como uma de suas maiores características era ser prudente, de início, apresentou sua teoria como mera hipótese, já que naquela época eram comuns, as condenações por heresia.
As revelações
Copérnico, era eclesiástico, respeitava e temia as autoridades religiosas, para estas, a teoria de Ptolomeu era mais adequada para confirmar, as citações bíblicas, de modo conveniente para a igreja. Temendo contradizê-la, Copérnico, em 1530, apresentou sua teoria apenas entre os astrônomos, num manuscrito chamado Pequenos comentários de Nicolau Copérnico em torno de suas hipóteses sobre os movimentos celestes. Somente em 1540, permitiu que George Joaquim Rhäticus, seu discípulo, publicasse suas idéias, na obra Narrativa acerca das obras de Copérnico sobre revoluções.
Sua obra
Finalmente em 1543, esse mesmo discípulo, fez circular, em Nuremberg, a obra completa de Copérnico - Sobre a revolução das orbes celestes, onde a Teoria Heliocêntrica, era colocada de forma científica, e não como hipótese. Isto se deu sem o conhecimento de Copérnico, que teve exemplar nas mãos, já pronto, às portas de sua morte, em Frauenburg, à 24/05/1543, mesma data em que veio a falecer. Esta publicação, que tinha prefácio dedicado ao papa Paulo III, fora substituído por outro, anônimo, atribuído a Andreas Osiander, que insistia sobre o carater hipotético do novo sistema.
Só após 20 anos da divulgação da pesquisa de Copérnico, o frade dominicano Giordani Bruno acrescentou a Teoria, a idéia do Universo infinito, levantando novamente a polêmica. Por isso, a Inquisição, o condenou a morte. Justo nessa mesma época, iniciava como professor de Universidade Galileu Galilei, que finalmente fez solidificar a Teoria .
A obra de Copérnico foi comprovada por grandes astrônomos e matemáticos como Galileu, Kepler e Newton, mas até 1835, a Igreja a manteve em sua lista negra. Mas sua obra, considerada valiosa e pioneira lhe garantiu a posição de Pai da Astronomia Moderna.