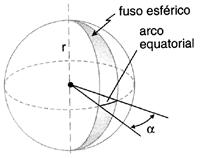
Nesta entrada afirmei que só existiam cinco poliedros regulares convexos, com faces iguais, os chamados sólidos platónicos, cuja justificação se podia deduzir da relação de Euler. Mas é preciso estabelecer condições adicionais que estes sólidos verificam. É o que explico a seguir, na chamada prova topológica.
A equação que relaciona o número de faces 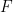 , vértices
, vértices 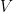 e arestas
e arestas  de um poliedro
de um poliedro
 , (1)
, (1)
aplicada ao cubo (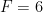 faces,
faces,  vértices,
vértices,  arestas), traduz-se na igualdade
arestas), traduz-se na igualdade

e, aplicada ao tetraedro, que é uma pirâmide equilátera (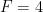 faces,
faces,  vértices,
vértices, 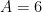 arestas), em
arestas), em
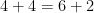 .
.
Num poliedro regular convexo (um segmento de recta que una quaisquer dois dos seus pontos não sai para fora do poliedro), em que cada face tem  lados iguais, se multiplicar o número de faces
lados iguais, se multiplicar o número de faces 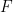 por estes
por estes  lados, conto as arestas duas vezes. Porquê? Porque cada aresta é a intersecção de duas faces adjacentes. No caso do cubo, em que as faces são quadrados (
lados, conto as arestas duas vezes. Porquê? Porque cada aresta é a intersecção de duas faces adjacentes. No caso do cubo, em que as faces são quadrados ( ) isto traduz-se em:
) isto traduz-se em:
 .
.
Para o tetraedro, cujas faces são triângulos equiláteros ( lados), pelo mesmo motivo, se multiplicar o número de faces por estes
lados), pelo mesmo motivo, se multiplicar o número de faces por estes 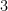 lados , obtenho
lados , obtenho
 .
.
No caso geral de um poliedro regular convexo, em que cada face tem  lados iguais, devido à dupla contagem será então:
lados iguais, devido à dupla contagem será então:
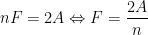 .
.
Voltando ao cubo, em que cada vértice é o ponto de encontro de  arestas, se multiplicar agora o número de vértices por estas
arestas, se multiplicar agora o número de vértices por estas 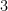 arestas, obtenho o dobro do número de arestas, porque também estou a contar cada aresta duas vezes, em virtude de cada aresta unir dois vértives:
arestas, obtenho o dobro do número de arestas, porque também estou a contar cada aresta duas vezes, em virtude de cada aresta unir dois vértives:
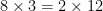 .
.
Fazendo o mesmo para o tetraedro,  , obtenho, pelo mesmo motivo
, obtenho, pelo mesmo motivo
 .
.
O caso geral, em que cada vértice de um poliedro regular convexo é o ponto de encontro de 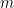 arestas, traduz-se em
arestas, traduz-se em
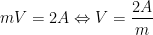 .
.
Assim, um poliedro regular convexo verifica a dupla igualdade
 , (2)
, (2)
em que  é o número inteiro de lados de cada face poligonal e
é o número inteiro de lados de cada face poligonal e 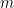 o número inteiro de arestas que se intersectam em cada vértice, pelo que a equação (1) é equivalente a
o número inteiro de arestas que se intersectam em cada vértice, pelo que a equação (1) é equivalente a
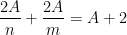
ou a
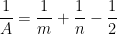 . (3)
. (3)
Esta equação corresponde, no caso particular do cubo a

e no do tetraedro a
 .
.
Mas há duas restrições aos possíveis valores inteiros de 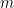 e
e  : uma, em virtude do número de arestas ser positivo, é
: uma, em virtude do número de arestas ser positivo, é
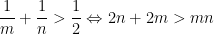 (4)
(4)
e a outra, porque o poliedro é um sólido tridimensional,
 . (5)
. (5)
O número de lados  de cada face define a sua forma poligonal: para
de cada face define a sua forma poligonal: para  é o triângulo equilátero,
é o triângulo equilátero,  , o quadrado,
, o quadrado, 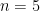 , o pentágono regular. Será que num poliedro regular convexo
, o pentágono regular. Será que num poliedro regular convexo  poderá ser igual a
poderá ser igual a 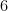 ? Vamos ver que não.
? Vamos ver que não.
Para  a equação (3) assume o valor particular
a equação (3) assume o valor particular
 .
.
e, pela restrição (4)
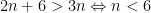
conclui-se que  . Os dois casos vistos acima são o tetraedro, que corresponde a
. Os dois casos vistos acima são o tetraedro, que corresponde a  e o cubo, a
e o cubo, a  . Para
. Para 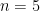 , vem
, vem
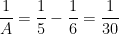
donde  ,
, 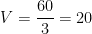 e
e 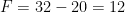 . Este poliedro regular com
. Este poliedro regular com 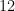 faces é o conhecido dodecaedro.
faces é o conhecido dodecaedro.
Para 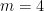 , a mesma equação (3) passa a ser
, a mesma equação (3) passa a ser

e agora a restrição (4),
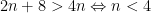 ,
,
isto é,  . O número de arestas, vértices e faces são, respectivamente,
. O número de arestas, vértices e faces são, respectivamente,  ,
,  e
e 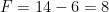 . É o octaedro, com oito faces que são triângulos equiláteros.
. É o octaedro, com oito faces que são triângulos equiláteros.
Para 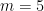 , (3) é a equação
, (3) é a equação
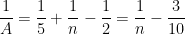
e a condição (4)
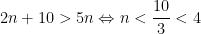
logo, é também  . O número de arestas, vértices e faces são, respectivamente,
. O número de arestas, vértices e faces são, respectivamente,  ,
, 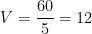 e
e 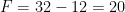 . É o icosaedro, com vinte faces que são triângulos equiláteros.
. É o icosaedro, com vinte faces que são triângulos equiláteros.
Para 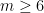 , a primeira forma de (4)
, a primeira forma de (4)

permite estabelecer
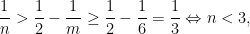
o que contraria a restrição
(5). Isto prova que  e que só há os cinco sólidos platónicos atrás referidos.
e que só há os cinco sólidos platónicos atrás referidos.

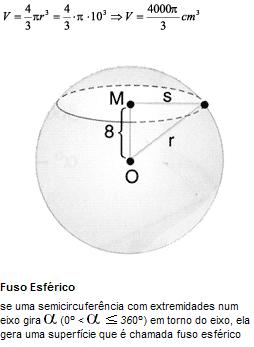
 Área da esfera
Área da esfera
![]() =
=![]() . s2 →s = 6cm
. s2 →s = 6cm![]() r2 = 4
r2 = 4![]() . 102 →A = 400
. 102 →A = 400![]() cm2
cm2