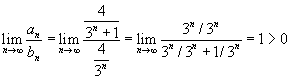Os cálculos percentuais estão presentes em situações cotidianas e nos exames de classificação de diversas universidades. Observe o exercício a seguir, ele exige conhecimentos de porcentagem, cálculos estatísticos, espaço amostral, representação de frequência relativa, cálculo de probabilidade e processos de contagem.
Uma empresa de táxis tem como meta atender em, no máximo, 20 minutos pelo menos 94% das chamadas que recebe. O controle dessa meta é feito de forma ininterrupta por um funcionário que utiliza um aparelho de rádio para monitoramento. A cada 100 chamadas, ele registra o número acumulado de chamadas que não foram atendidas em 20 minutos. Ao final de um dia, a cooperativa apresenta o seguinte desempenho:
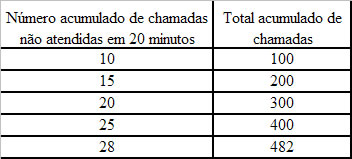
Com base no enunciado do exercício, o número de chamadas não atendidas em 15 minutos não deve ultrapassar 6%.
Estabelecendo a freqüência relativa
Razões: 10/100, 15/200, 20/300, 25/400, 28/482.
10/100 = 0,1 = 10% > 6% → acima
15/200 = 0,075 = 7,5% > 6% → acima
20/300 = 0,066 = 6,6% > 6% → acima
25/400 = 0,0625 = 6,25% > 6% → acima
28/482 = 0,058 = 5,8% < 6% → meta atingida
Concluímos que a meta somente foi cumprida quando o total de chamadas acumuladas resultou em 482.
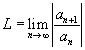 . Então:
. Então: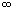 ), a série é DIVERGENTE.
), a série é DIVERGENTE.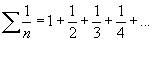 é chamada SÉRIE HARMÔNICA e, de acordo com o teorema, é divergente.
é chamada SÉRIE HARMÔNICA e, de acordo com o teorema, é divergente. 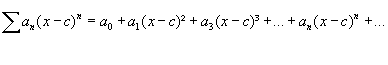
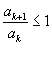 .
.