

A definição dos entes primitivos ponto, reta e plano é quase impossível, o que sabe-se muito bem e aqui será o mais importante é sua representação geométrica e espacial.
Representação, (notação)
→ Pontos serão representados por letras latinas maiúsculas; ex: A, B, C,…
→ Retas serão representados por letras latinas minúsculas; ex: a, b, c,…
→ Planos serão representados por letras gregas minúsculas; ex:
Representação gráfica



Postulados primitivos da geometria, qualquer postulado ou axioma é aceito sem que seja necessária a prova, contanto que não exista a contraprova.
1º Numa reta bem como fora dela há infinitos pontos distintos.
2º Dois pontos determinam uma única reta (uma e somente uma reta).

3º Pontos colineares pertencem à mesma reta.

4º Três pontos determinam um único plano.

5º Se uma reta contém dois pontos de um plano, esta reta está contida neste plano.

6º Duas retas são concorrentes se tiverem apenas um ponto em comum.

Observe que  . Sendo que H está contido na reta r e na reta s.
. Sendo que H está contido na reta r e na reta s.
Denominamos ângulo a região do plano limitada por duas semirretas de mesma origem. As semirretas recebem o nome de lados do ângulo e a origem delas, de vértice do ângulo.

A unidade usual de medida de ângulo, de acordo com o sistema internacional de medidas, é o grau, representado pelo símbolo º, e seus submúltiplos são o minuto ’ e o segundo ”.
Temos que 1º (grau) equivale a 60’ (minutos) e 1’ equivale a 60”(segundos).
O objeto capaz de medir o valor de um ângulo é chamado de transferidor, podendo ele ser de “meia volta” (180º) ou volta inteira (360º).
Classificação de ângulos
Os ângulos são classificados de acordo com suas medidas:
Agudo: ângulo com medida menor que 90º.
Reto: ângulo com medida igual a 90º.
Obtuso: ângulo com medida maior que 90º.
Raso: ângulo com medida igual a 0º ou 180º.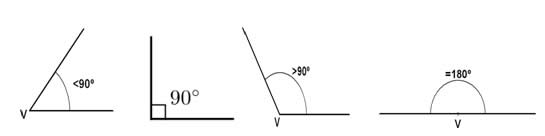
agudo reto obtuso raso
Bissetriz de um ângulo
Bissetriz de um ângulo pode ser definida como a semirreta que se origina no vértice do ângulo principal, dividindo-o em outros dois ângulos com medidas iguais.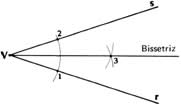
Retas paralelas cortadas por uma transversal
Ângulos correspondentes: a e e, d e h, b e f, c e g Congruentes
Ângulos colaterais externos: a e h, b e g Suplementares
Ângulos colaterais internos: e e d, c e f Suplementares
Ângulos alternos externos: a e g, b e h Congruentes
Ângulos alternos internos: d e f, c e e Congruentes
Por Marcos Noé
Graduado em Matemática
Equipe Brasil Escola