Poliedros

Poliedros

Superfície poliédrica

Chama-se superfície poliédrica a junção de um número limitado n (n ∈ N*) de polígonos planos, assim:

a-) Jamais são clopanares, dois polígonos com um lado em comum;
b-) Cada lado do polígono esta no máximo em dois polígonos.
c-) Qualquer polígono tem ao menos um lado comum com dos outros polígonos.

Elementos

Obtemos em numa superfície poliédrica, as faces que são os polígonos, as arestas que são as laterais dos polígonos e os vértices, que são os vértices dos polígonos. Assim,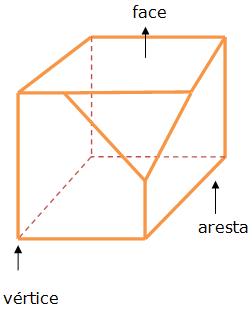



• A aresta que é lado de um único polígono é denominada aresta livre.
• Já a aresta que é lado de dois polígonos é denominada aresta dupla.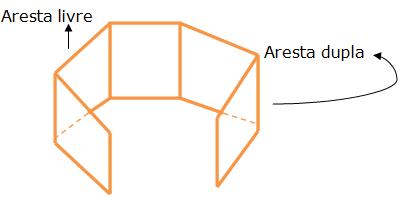




Superfície poliédrica aberta

Classificação

A superfície poliédrica que tem aresta livre é denominada superfície poliédrica aberta. Já a que não possui a aresta livre é denominada superfície poliédrica fechada.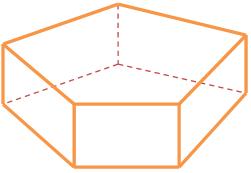


Superfície poliédrica fechada

Superfície poliédrica convexa

Sempre que o plano de cada polígono deixa todos os demais polígonos num mesmo semi- espaço este é denominado superfície poliédrica convexa.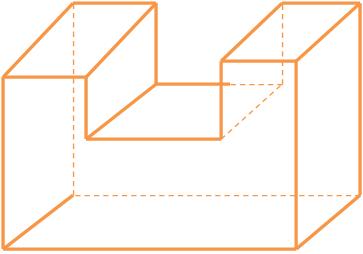


Superfície poliédrica não convexa

Poliedro

O poliedro é ponto do espaço demarcado por uma superfície poliédrica fechada. O poliedro demarcado pela superfície poliédrica convexa é denominado poliedro convexo.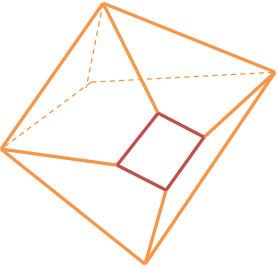



Poliedro convexo

Relações de Euler

I) Dada uma superfície poliédrica convexa aberta com vértices (V), arestas (A) e faces (F), teremos:



II) Dada uma superfície poliédrica convexa fechada com vértices (V), arestas (A) e faces (F), teremos:



Chamamos de poliedro Eureliano, qualquer poliedro que sacie essa relação.

Observação:

“Todo poliedro convexo é Eureliano, mas nem todo poliedro Eureliano é convexo”.

Note que o poliedro abaixo não é convexo, mas segue a relação V – A + F =2.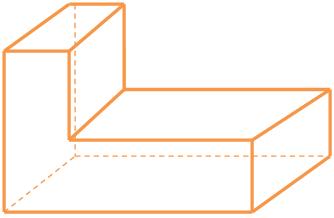




Soma dos ângulos das faces

Em todo poliedro convexo de vértices (V), a soma dos ângulos de todas as suas faces é dada por:

http://www.colegioweb.com.br/matematica/poliedros.html