Adição e Subtração de Arcos= - Trigonometria II

Considerando a e b como sendo as determinações de dois arcos, temos:

• Cosseno de (a + b)


Demonstração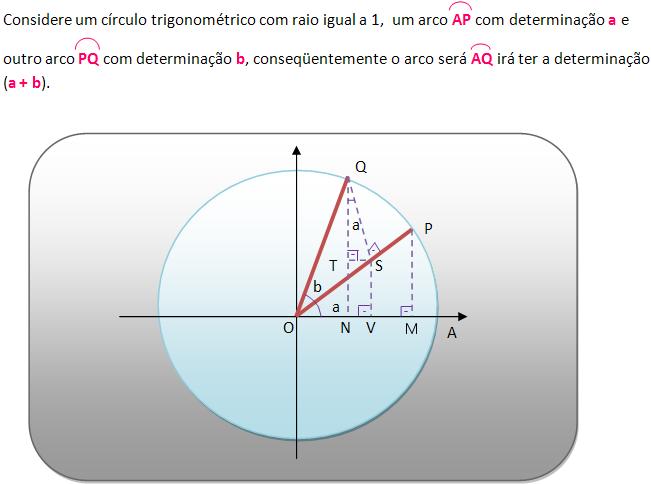


Baseados nas construções geométricas mostradas na representação acima, concluímos que os triângulos OMP, OVS e QTS são retângulos e muito parecidos, ou seja:

I) OM = cos a
PM = sen a
OS = cos b
QS = sen b
ON = cos (a + b)



Como:
ON = OV – NV = OV – TS, resulta em: cos (a + b) = cos a . cos b – sen a . sen b

• Cosseno de (a – b)


Demonstração
Como cos ( – b) = cos b
sen ( – b) = sen b, temos:
cos (a – b) = cos [a + (– b)] =
= cos a . cos (– b) – sen a . sen (– b) =
= cos a . cos b + sen a . sen b

• Seno de (a + b)







• Seno de (a – b)


Demonstração
Como cos (– b) = cos b
sen (– b) = – sen b temos:
sen (a – b) = sen [a + (– b)] =
= sen a . cos (– b) + cos a . sen (– b) =
= sen a . cos b – cos a . sen b

• Tangente de (a + b)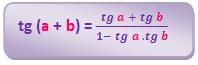






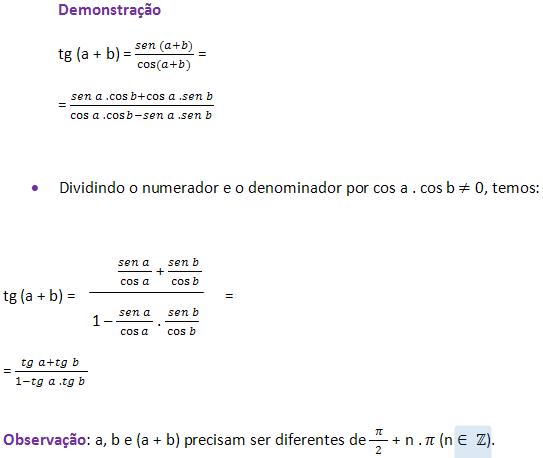
• Tangente de (a – b)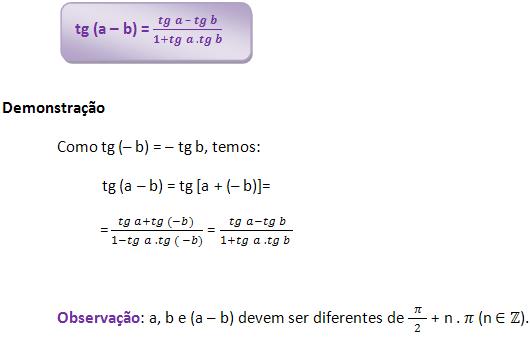

2. ARCO DUPLO

Usaremos as fórmulas da soma e da subtração de dois arcos para obter as fórmulas do arco duplo.

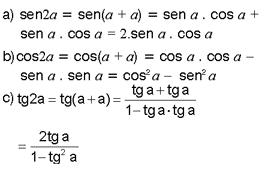
Aplicação


3. TRANSFORMAÇÃO EM PRODUTO

As fórmulas de adição e subtração de arcos podem ser transformadas em produtos a partir de:



Aplicação
Transformar em produto a expressão y = sen 40° + sen 30°.

Solução:

m = 40° e n = 30°

Aplicando a forma fatorada de sen m + sen n, temos:



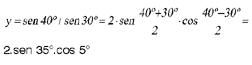
4. EQUAÇÕES TRIGONOMÉTRICAS
É toda equação em que figura uma função trigonométrica com arco desconhecido. Chamam-se soluções de uma equação trigonométrica os valores da variável, caso existam, que satisfazem a equação dada.

Exemplos:

a) sen x = – 1

b) cos x = 0




Fórmulas da Adição


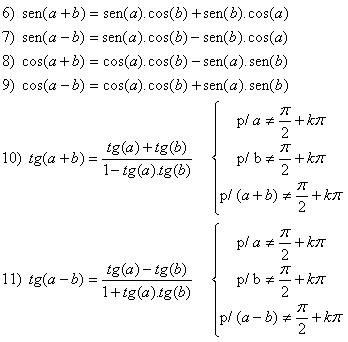
As fórmulas acima são verdadeiras para arcos positivos, cujo a soma pertence ao primeiro quadrante.

Fórmulas da Multiplicação

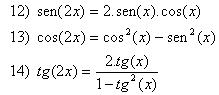
Aplicação



5. INEQUAÇÕES TRIGONOMÉTRICAS

Uma inequação trigonométrica é uma desigualdade em que aparecem funções trigonométricas da incógnita.

Exemplos:



Aplicação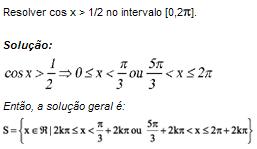

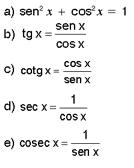
As relações entre os valores das funções trigonométricas de um mesmo arco são denominadas relações trigonométricas.



Observações:

a) cotg x = co-tangente de x

b) sec x = secante de x

c) cosec x = co-ssecante de x

Aplicação
Simplificar a expressão:

1 – sen x . cos x . tg



Aplicação

Calcular sen 75°.

Solução:

Podemos observar que 75º = 30º + 45º; logo sen 75º = sen (30º + 45º). A partir da fórmula, temos:

sen (30º + 45º) = sen 30º. cos 45º + sen 45º . cos 30º =

Fonte: http://www.colegioweb.com.br/matematica/adicao-e-subtracao-de-arcos-.html