TEOREMA

TEOREMA

Se a série converge, então

OBS: * A recíproca desse teorema é falsa, isto é, existem séries cujo termo genérico tende a zero e que não são convergentes.

* Vale a contrapositiva: "se o limite não é zero, então a série não converge", que constitui o:

TESTE DA DIVERGÊNCIA Dada a série , diverge.

SÉRIE GEOMÉTRICA

TIPO: com a0

r é a razão.

Ex: 1 + 2 + 4 + 8 + 16 + ...

a = 1

r =

SOMA DE UMA SÉRIE GEOMÉTRICA

A série geométrica

Converge e tem soma se | r | <>

Diverge se | r | 1.

TESTE DA COMPARAÇÃO

Sejam e duas séries de termos positivos. Então:

* Se , sendo "c" um número real, então as séries são ambas convergentes ou ambas divergentes.

* Se e se converge, então também converge.

* Se e se diverge, então também diverge.

OBS: Se a_n é expressa por uma fração, devemos considerar tanto no numerador, quanto no denominador de b_n somente os termos de maior importância.

Ex: Verifique se a série dada converge ou diverge:

é uma série geométrica de razão 1/3, logo ela é convergente. Aplicando o teste da comparação, temos:

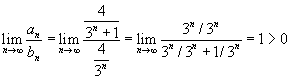
Logo, conclui-se que a série CONVERGE.