Cofator
Chamamos de cofator ou complemento algébrico relativo a um elemento aij de uma matriz quadrada de ordem n o número Aij tal que Aij = (-1)i+j . MCij .
Veja:
a) Dada 
, os cofatores relativos aos elementos a11 e a12 da matriz M são:
|
|
|
b) Sendo 
, vamos calcular os cofatores A22, A23 e A31:
|
|
|
|
|
|
Teorema de Laplace
O determinante de uma matriz quadrada M = [aij]mxn 
pode ser obtido pela soma dos produtos dos elementos de uma fila qualquer ( linha ou coluna) da matriz M pelos respectivos cofatores.
Assim, fixando 
, temos:
em que 
é o somatório de todos os termos de índice i, variando de 1 até m, 
.
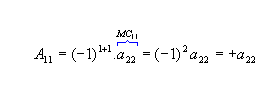
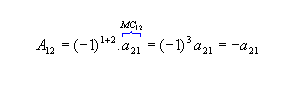
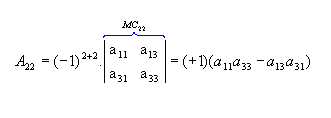
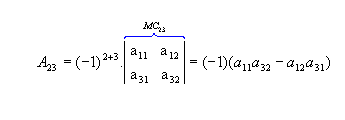
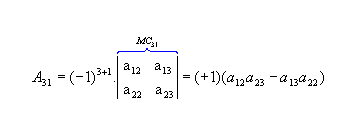
Nenhum comentário:
Postar um comentário