Dados os pontos P=(x1,y1) e Q=(x2,y2), obtem-se a distância entre P e Q, traçando-se projeções destes pontos sobre os eixos coordenados e identificando um triângulo retângulo no gráfico e a partir daí, utiliza-se o Teorema de Pitágoras.
O segmento PQ será a hipotenusa do triângulo retângulo PQR, o segmento PR será um cateto e o segmento QR será o outro cateto, logo:
então
Exemplos
A distância entre P=(2,3) e Q=(5,12) é
A distância entre a origem O=(0,0) e um ponto genérico P=(x,y) é dada por
Consideremos um plano e duas retas perpendiculares, sendo uma delas horizontal e a outra vertical. A horizontal será denominada Eixo das Abscissas (ou eixo OX) e a Vertical será denominada Eixo das Ordenadas (ou eixo OY).
Os pares ordenados de pontos do plano são indicados na forma geral P=(x,y) onde x será a abscissa do ponto P e y a ordenada do ponto P.
Na verdade, x representa a distância entre as duas retas verticais indicadas no gráfico e y é a distância entre as duas retas horizontais indicadas no gráfico.
O sistema de Coordenadas Ortogonais também é conhecido por Sistema de Coordenadas Cartesianas.
Este sistema possui quatro (4) regiões denominadas quadrantes.
| Quadrante | Sinal de x | Sinal de y | Exemplo |
Determinantes
P10) Quando, em uma matriz, os elementos acima ou abaixo da diagonal secundária são todos nulos, o determinante é igual ao produto dos elementos dessa diagonal multiplicado por 
.
Exemplos:
 |  |
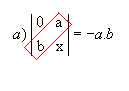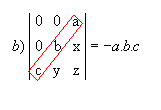P11) Para A e B matrizes quadradas de mesma ordem n, 
. Como: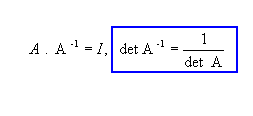 
Exemplo:
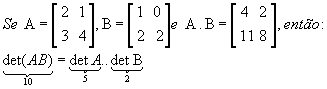
P12) 
Exemplo:
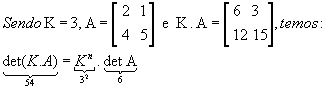
Determinantes
P6) O determinante de uma matriz e o de sua transposta são iguais.
Exemplo:
 |  |
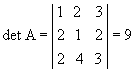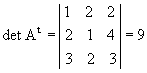P7) Multiplicando por um número real todos os elementos de uma fila em uma matriz, o determinante dessa matriz fica multiplicado por esse número.
Exemplos:
 |
 |
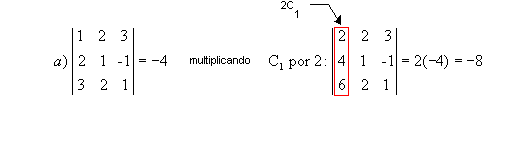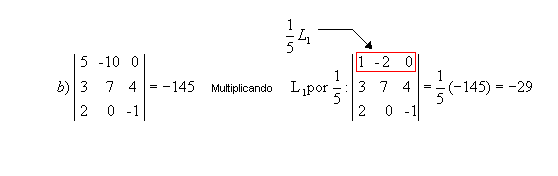P8) Quando trocamos as posições de duas filas paralelas, o determinante de uma matriz muda de sinal.
Exemplo:
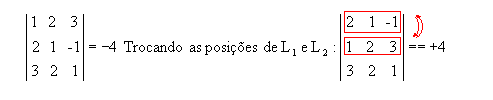
P9) Quando, em uma matriz, os elementos acima ou abaixo da diagonal principal são todos nulos, o determinante é igual ao produto dos elementos dessa diagonal.
Exemplos:
  |
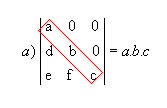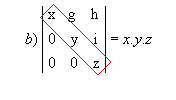Propriedades dos determinantes
Os demais associados a matrizes quadradas de ordem n apresentam as seguintes propriedades:
P1 ) Quando todos os elementos de uma fila ( linha ou coluna) são nulos, o determinante dessa matriz é nulo.
Exemplo:
 |  |
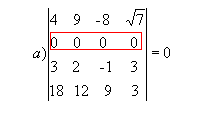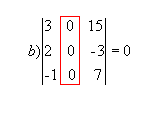P2) Se duas filas de uma matriz são iguais, então seu determinante é nulo.
Exemplo:
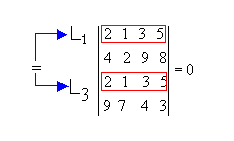
P3) Se duas filas paralelas de uma matriz são proporcionais, então seu determinante é nulo.
Exemplo:
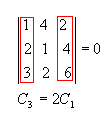
P4) Se os elementos de uma fila de uma matriz são combinações lineares dos elementos correspondentes de filas paralelas, então seu determinante é nulo.
Exemplos:
 |  |
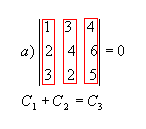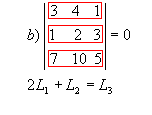P5 ) Teorema de Jacobi: o determinante de uma matriz não se altera quando somamos aos elementos de uma fila uma combinação linear dos elementos correspondentes de filas paralelas.
Exemplo:
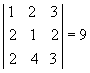
Substituindo a 1ª coluna pela soma dessa mesma coluna com o dobro da 2ª, temos:
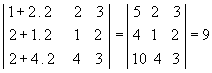
6ª propriedade
O valor do determinante de uma matriz R é igual ao determinante da matriz da transposta de R, det R = det (R t).
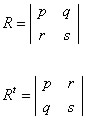
det R = ps + qr
det Rt = ps – rq
7ª propriedade
Ao trocarmos duas linhas ou duas colunas de posição de uma matriz, o valor do seu determinante passa a ser oposto ao determinante da anterior.
8ª propriedade
O determinante de uma matriz triangular é igual à multiplicação dos elementos da diagonal principal.
Lembre-se que em uma matriz triangular, os elementos acima ou abaixo da diagonal principal são iguais a zero.
Regra de Sarrus
O cálculo do determinante de 3ª ordem pode ser feito por meio de um dispositivo prático, denominado regra de Sarrus.
Acompanhe como aplicamos essa regra para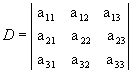 
.
1º passo: Repetimos as duas primeiras colunas ao lado da terceira:
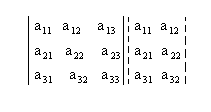
2º passo: Encontramos a soma do produto dos elementos da diagonal principal com os dois produtos obtidos pela multiplicação dos elementos das paralelas a essa diagonal (a soma deve ser precedida do sinal positivo):
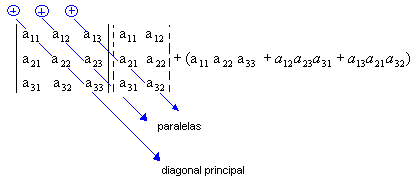
3º passo: Encontramos a soma do produto dos elementos da diagonal secundária com os dois produtos obtidos pela multiplicação dos elementos das paralelas a essa diagonal ( a soma deve ser precedida do sinal negativo):
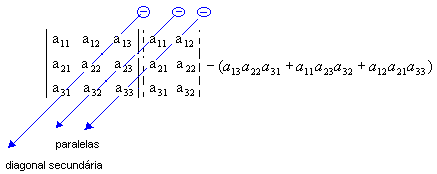
Assim:
Observação: Se desenvolvermos esse determinante de 3ª ordem aplicando o Teorema de Laplace, encontraremos o mesmo número real.
Determinante de ordem n > 3
Vimos que a regra de Sarrus é válida para o cálculo do determinante de uma matriz de ordem 3. Quando a matriz é de ordem superior a 3, devemos empregar o Teorema de Laplace para chegar a determinantes de ordem 3 e depois aplicar a regra de Sarrus.
Cofator
Chamamos de cofator ou complemento algébrico relativo a um elemento aij de uma matriz quadrada de ordem n o número Aij tal que Aij = (-1)i+j . MCij .
Veja:
a) Dada 
, os cofatores relativos aos elementos a11 e a12 da matriz M são:
|
|
|
b) Sendo 
, vamos calcular os cofatores A22, A23 e A31:
|
|
|
|
|
|
Teorema de Laplace
O determinante de uma matriz quadrada M = [aij]mxn 
pode ser obtido pela soma dos produtos dos elementos de uma fila qualquer ( linha ou coluna) da matriz M pelos respectivos cofatores.
Assim, fixando 
, temos:
em que 
é o somatório de todos os termos de índice i, variando de 1 até m, 
.
