MATEMÁTICA CURIOSA: Números Complexos

Os números complexos são escritos na sua forma algébrica da seguinte forma: a + bi, sabemos que a e b são números reais e que o valor de a é a parte real do número complexo e que o valor de bi é a parte imaginária do número complexo.

Podemos então dizer que um número complexo z será igual a a + bi (z = a + bi).

Com esses números podemos efetuar as operações de adição, subtração e multiplicação, obedecendo à ordem e características da parte real e parte imaginária.

Adição

Dado dois números complexos quaisquer z1 = a + bi e z2 = c + di, ao adicionarmos teremos:

z1 + z2
(a + bi) + (c + di)

a + bi + c + di

a + c + bi + di

a + c + (b + d)i

(a + c) + (b + d)i

Portanto, z1 + z2 = (a + c) + (b + d)i.

Exemplo:
Dado dois números complexos z1 = 6 + 5i e z2 = 2 – i, calcule a sua soma:

(6 + 5i) + (2 – i)
6 + 5i + 2 – i
6 + 2 + 5i – i
8 + (5 – 1)i
8 + 4i

Portanto, z1 + z2 = 8 + 4i.

Subtração

Dado dois números complexos quaisquer z1 = a + bi e z2 = c + di, ao subtraímos teremos:

z1 - z2
(a + bi) - (c + di)

a + bi – c – di

a – c + bi – di

(a – c) + (b – d)i

Portanto, z1 - z2 = (a - c) + (b - d)i.

Exemplo:
Dado dois números complexos z1 = 4 + 5i e z2 = -1 + 3i, calcule a sua subtração:

(4 + 5i) – (-1 + 3i)
4 + 5i + 1 – 3i
4 + 1 + 5i – 3i
5 + (5 – 3)i
5 + 2i

Portanto, z1 - z2 = 5 + 2i.

Multiplicação

Dado dois números complexos quaisquer z1 = a + bi e z2 = c + di, ao multiplicarmos teremos:

z1 . z2
(a + bi) . (c + di)

ac + adi + bci + bdi2
ac + adi + bci + bd (-1)
ac + adi + bci – bd
ac - bd + adi + bci
(ac - bd) + (ad + bc)i

Portanto, z1 . z2 = (ac + bd) + (ad + bc)I.

Exemplo:

Dado dois números complexos z1 = 5 + i e z2 = 2 - i, calcule a sua multiplicação:

(5 + i) . (2 - i)
5 . 2 – 5i + 2i – i²
10 – 5i + 2i + 1
10 + 1 – 5i + 2i
11 – 3i

Portanto, z1 . z2 = 11 – 3i.

Ao dividirmos dois números complexos devemos escrevê-los em forma de fração e multiplicarmos o numerador e o denominador pelo conjugado do denominador, veja como:

Dado dois números complexos z₁ e z₂, para efetuarmos a divisão dos dois devemos seguir a seguinte regra:
z₁ : z₂ = z₁.

z₂

De uma forma geral podemos demonstrar a divisão de dois números complexos por:

Dado z1 = a + bi e z2 = c + di a divisão de z1 : z2 será:

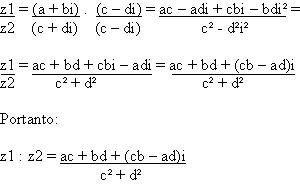
abemos que um número complexo possui forma geométrica igual a z = a + bi, onde a recebe a denominação de parte real e b parte imaginária de z. Por exemplo, para o número complexo z = 3 + 5i, temos a = 3 e b = 5 ou Re(z) = 3 e Im(z) = 5. Os números complexos também possuem uma forma trigonométrica ou polar, que será demonstrada com base no argumento de z (para z ≠ 0).
Considere o número complexo z = a + bi, em que z ≠ 0, dessa forma temos que: cosӨ = a/p e senӨ = b/p. Essa relações podem ser escritas de outra forma, acompanhe:

cosӨ = a/p → a = p*cosӨ

senӨ = b/p → b = p*senӨ

Vamos substituir os valores de a e b no complexo z = a + bi.

z = p*cosӨ + p*senӨi → z = p*( cosӨ + i*senӨ)

Essa forma trigonométrica é de grande utilidade nos cálculos envolvendo potenciações e radiciações.

Exemplo 1
Represente o número complexo z = 1 + i na forma trigonométrica.
Resolução:
Temos que a = 1 e b = 1

A forma trigonométrica do complexo z = 1 + i é z = √2*(cos45º + sen45º * i).

Exemplo 2
Represente trigonometricamente o complexo z = –√3 + i.
Resolução:
a = –√3 e b = 1

A forma trigonométrica do complexo z = –√3 + i é z = 2*(cos150º + sen150º * i).

O inverso de um número é a troca do numerador pelo denominador e vice-versa, desde que essa fração ou número seja diferente de zero. Em um número complexo acontece da mesma forma: um número complexo para ter seu inverso é preciso ser não nulo, por exemplo:

Dado um número complexo qualquer não nulo z = a + bi, o seu inverso será representado por z^–1.

Veja o cálculo do inverso do número complexo z = 1 – 4i.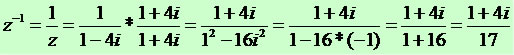

Portanto, o inverso do número complexo z = 1 – 4i será: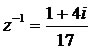

Concluímos que o inverso de um número complexo não nulo terá a seguinte generalidade: z = a + bi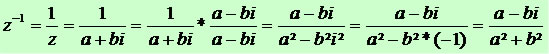

Quando multiplicamos um número complexo pelo seu inverso o resultado será sempre igual a 1, z * z^–1 = 1. Observe a multiplicação do complexo z = 1 – 4i pelo seu inverso: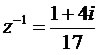

A multiplicação de números complexos ocorre da seguinte maneira:

(a+bi)*(c +di) = ac + adi + bci + bdi² = ac + (ad + bc)i + bd(–1) = ac + (ad + bc)i – bd = (ac – bd) + (ad + bc)i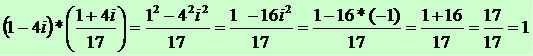

Ao resolver uma equação do 2º grau podemos obter três resultados, dependendo do valor do discriminante:
∆ > 0, duas raízes reais diferentes.
∆ = 0, uma raiz real.
∆ < i =" -" z =" (x,y)" z =" a" z =" 2" z =" 5" 25 =" 0" 81 =" 0" x =" ±√–81" x =" ±9i" 50 =" 0" a =" 2," b =" -16," c =" 50" alt="" src="http://www.brasilescola.com/upload/e/8%286%29.jpg" height="134" width="108">

x’ = 4 + 3i e x’’ = 4 – 3i

Consideremos o número complexo não nulo z = p*(cosӨ + i*senӨ) e o número n Є N, dessa forma escrevemos:

zⁿ = z*z*z*...*z ou zⁿ = p*p*p*...*p *(cosӨ + i*senӨ)* (cosӨ + i*senӨ).... (cosӨ + i*senӨ), daí, zⁿ = pⁿ*[cos(Ө+Ө+Ө+...+Ө) + i*sen(Ө+Ө+Ө+...+Ө)], onde concluímos que:

zⁿ = pⁿ *[cos(nӨ) + i*sen(nӨ)]

Essa expressão é um recurso muito importante nas situações envolvendo a expressão (a + bi)n, caso não existisse, deveríamos usar o binômio de Newton, o que acarretaria em cálculos trabalhosos.

Obs.: para calcularmos a potência de um número complexo utilizando a 1º fórmula de Moivre, devemos escrever o complexo na sua forma trigonométrica.

Exemplo 1
Dado o complexo z = – 2 – 2i, calcule z¹⁰.

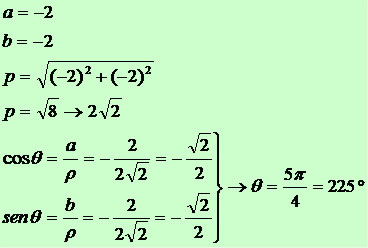
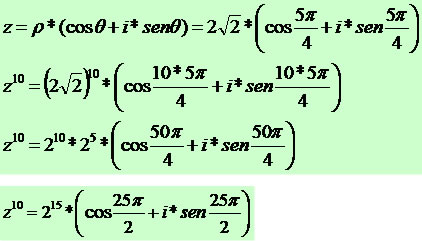
Exemplo 2
Dado o número complexo z = –1 –√3i, determine z¹⁵.

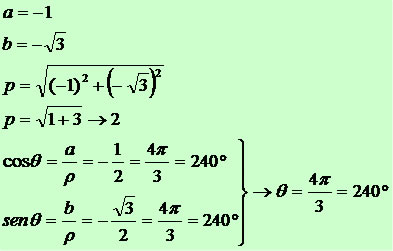
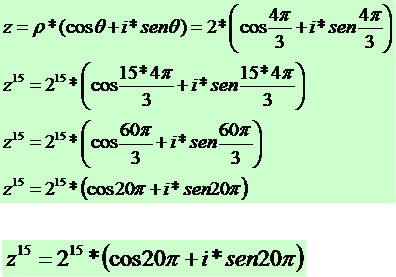
Para determinarmos o oposto, o conjugado e a igualdade de qualquer número complexo precisamos conhecer alguns fundamentos.

Oposto

O oposto de qualquer número real é o seu simétrico, o oposto de 10 é -10, o oposto de -5 é +5. O oposto de um número complexo respeita essa mesma condição, pois o oposto do número complexo z será – z.

Por exemplo: Dado o número complexo z = 8 – 6i, o seu oposto será:
- z = - 8 + 6i.

Conjugado

Para determinarmos o conjugado de um número complexo, basta representar o número complexo através do oposto da parte imaginária. O conjugado de z = a + bi será:

Exemplo:
z = 5 – 9i, o seu conjugado será:

z = – 2 – 7i, o seu conjugado será

Igualdade

Dois números complexos serão iguais se, e somente se, respeitarem a seguinte condição:
Partes imaginárias iguais
Partes reais iguais

Dado os números complexos z1 = a + bi e z2 = d + ei, z1 e z2, serão iguais se, somente se, a = d e bi = ei.

Observações:

A soma de números complexos opostos será sempre igual a zero.
z + (-z) = 0.

O conjugado de um número complexo será o próprio número complexo.

Não existe relação de ordem no conjunto dos números complexos, então não podemos estabelecer quem é maior ou menor.

Exemplo 1

Dado o número complexo z = - 2 + 6i, calcule o seu oposto, o seu conjugado e o oposto do conjugado.

Oposto
- z = 2 - 6i

Conjugado