Desafio

Ao calcular o valor de :

Encontre o resultado?

a) 15

b) 0,25

c) 25

d) 5

POSTE SUA RESPOSTA NO COMENTÁRIOS

4. Conectivos lógicos

Conectivos lógicos são palavras usadas para conectar as proposições formando novas sentenças.

Os principais conectivos lógicos são:

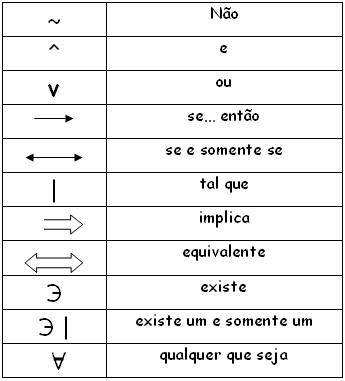
Equivalência lógica

Definição

Há equivalência entre as proposições P e Q somente quando a bicondicional P ↔ Q for uma tautologia ou quando P e Q tiverem a mesma tabela-verdade. P ⇔ Q (P é equivalente a Q) é o símbolo que representa a equivalência lógica.

Diferenciação dos símbolos ↔ e ⇔

O símbolo ↔ representa uma operação entre as proposições P e Q, que tem como resultado uma nova proposição P ↔ Q com valor lógico V ou F.

O símbolo ⇔ representa a não ocorrência de VF e de FV na tabela-verdade P ↔ Q, ou ainda que o valor lógico de P ↔ Q é sempre V, ou então P ↔ Q é uma tautologia.

Exemplo

A tabela da bicondicional (p → q) ↔ (~q → ~p) será:



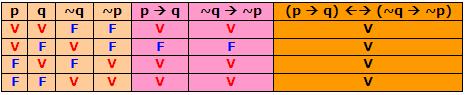
Portanto, p → q é equivalente a ~q → ~p, pois estas proposições possuem a mesma tabela-verdade ou a bicondicional (p → q) ↔ (~q → ~p) é uma tautologia.

Veja a representação:

(p → q) ⇔ (~q → ~p)

Implicação lógica

Definição

A proposição P implica a proposição Q, quando a condicional P → Q for uma tautologia.

O símbolo P ⇒ Q (P implica Q) representa a implicação lógica.

Diferenciação dos símbolos → e ⇒

O símbolo → representa uma operação matemática entre as proposições P e Q que tem como resultado a proposição P → Q, com valor lógico V ou F.

O símbolo ⇒ representa a não ocorrência de VF na tabela-verdade de P → Q, ou ainda que o valor lógico da condicional P → Q será sempre V, ou então que P → Q é uma tautologia.

Exemplo

A tabela-verdade da condicional (p Λ q) → (p ↔ q) será:



Portanto, (p Λ q) → (p ↔ q) é uma tautologia, por isso (p Λ q) ⇒ (p ↔q)

. O conectivo e e a conjunção

O conectivo e e a conjunção de duas proposições p e q é outra proposição que tem como valor lógico V se p e q forem verdadeiras, e F em outros casos. O símbolo p Λ q (p e q) representa a conjunção, com a seguinte tabela-verdade:



Exemplo

p = 2 é par
q = o céu é rosa

p Λ q = 2 é par e o céu é rosa



p = 9 < 6
q = 3 é par

p Λ q: 9 <>e 3 é par



p = O número 17 é primo
q = Brasília é a capital do Brasil

p Λ q = O número 17 é primo e Brasília é a capital do Brasil

O conectivo não e a negação

O conectivo não e a negação de uma proposição p é outra proposição que tem como valor lógico V se p for falsa e F se p é verdadeira. O símbolo ~p (não p) representa a negação de p com a seguinte tabela-verdade:



Exemplo:

p = 7 é ímpar
~p = 7 não é ímpar



q = 24 é múltiplo de 5
~q = 24 não é múltiplo de 5

O conectivo ou e a disjunção

O conectivo ou e a disjunção de duas proposições p e q é outra proposição que tem como valor lógico V se alguma das proposições for verdadeira e F se as duas forem falsas. O símbolo p ∨ q (p ou q) representa a disjunção, com a seguinte tabela-verdade:



Exemplo:

p = 2 é par
q = o céu é rosa
p ν q = 2 é par ou o céu é rosa



p = 9 < 6
q = 3 é par
p ν q: = 9 <>ou 3 é par



p = O número 17 é primo
q = Brasília é a capital do Brasil
p ν q = O número 17 é primo ou Brasília é a capital do Brasil



p = O número 9 é par
q = O dobro de 50 é 100
p ν q: O número 9 é par ou o dobro de 50 é 100

O conectivo se e somente se e a bicondicional

A bicondicional p se e somente se q é outra proposição que tem como valor lógico V se p e q forem ambas verdadeiras ou ambas falsas, e F nos outros casos.

O símbolo representa a bicondicional, com a seguinte tabela-verdade:



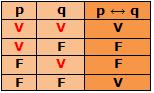
Exemplo

p = 24 é múltiplo de 3
q = 6 é ímpar
= 24 é múltiplo de 3 se, e somente se, 6 é ímpar.



p = 25 é quadrado perfeito
q = 8 > 3
= 25 é quadrado perfeito se, e somente se, 8 > 3



p = 27 é par
q = 6 é primo
= 27 é par se, e somente se, 6 é primo

O conectivo se... então... e a condicional

A condicional se p então q é outra proposição que tem como valor lógico F se p é verdadeira e q é falsa. O símbolo p → q representa a condicional, com a seguinte tabela-verdade:



Exemplo:

P: 7 + 2 = 9
Q: 9 – 7 = 2
p → q: Se 7 + 2 = 9 então 9 – 7 = 2



p = 7 + 5 < 4
q = 2 é um número primo
p → q: Se 7 + 5 <>então 2 é um número primo.



p = 24 é múltiplo de 3
q = 3 é par
p → q: Se 24 é múltiplo de 3 então 3 é par.



p = 25 é múltiplo de 2
q = 12 < 3
p → q: Se 25 é múltiplo de 2 então 2 < 3.

Operações lógicas com sentenças abertas

É possível efetuar as sentenças abertas de forma análoga à das proposições lógicas, através dos conectivos já apresentados: não, e, ou, se então, se e somente se.

Exemplo

Observando a condicional (x > 5) → (x > 2), em N, podemos notar que:

Proposições simples e compostas

As proposições simples ou atômicas são assim caracterizadas por apresentarem apenas uma idéia. São indicadas pelas letras minúsculas: p, q, r, s, t...

As proposições compostas ou moleculares são assim caracterizadas por apresentarem mais de uma proposição conectadas pelos conectivos lógicos. São indicadas pelas letras maiúsculas: P, Q, R, S, T...

Obs: A notação Q(r, s, t), por exemplo, está indicando que a proposição composta Q é formada pelas proposições simples r, s e t.

Exemplo:

Proposições simples:

p: O número 24 é múltiplo de 3.
q: Brasília é a capital do Brasil.
r: 8 + 1 = 3 . 3
s: O número 7 é ímpar
t: O número 17 é primo

Proposições compostas

P: O número 24 é divisível por 3 e 12 é o dobro de 24.
Q: A raiz quadrada de 16 é 4 e 24 é múltiplo de 3.
R(s, t): O número 7 é ímpar e o número 17 é primo.

Princípios fundamentais da lógica

Principio da não contradição: Uma proposição não pode ser verdadeira e falsa, ao mesmo tempo.

Principio do terceiro excluído: Uma alternativa só pode ser verdadeira ou falsa.

Proposição

Proposição ou sentença é um termo utilizado para exprimir idéias, através de um conjunto de palavras ou símbolos. Este conjunto descreve o conteúdo dessa idéia.

Sentenças abertas

Definições

Supondo que U seja um conjunto e x um elemento desse conjunto, podemos considerar que:

- U é um conjunto-universo e x a variável.

- a proposição p(x) será uma sentença aberta em U quando p(a) for verdadeira ou p(a) for falsa, ∀a ∈ U.

- se a ∈ U e p(a) for verdadeira, nesse caso a confirma p(x) ou a é a solução de p(x).

- O conjunto-verdade de p(x), em U, é formado por todos e somente os elementos de a ∈ U, onde p(a) é uma sentença verdadeira. Veja a representação deste conjunto: {a ∈ U| p(a) é V}.

Exemplos:

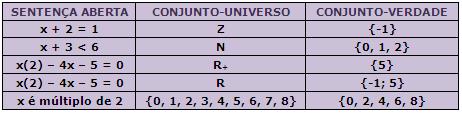
Tabela-Verdade

A tabela-verdade é usada para determinar o valor lógico de uma proposição composta, sendo que os valores das proposições simples já são conhecidos. Pois o valor lógico da proposição composta depende do valor lógico da proposição simples.

A seguir vamos compreender como se constrói essas tabelas-verdade partindo da árvore das possibilidades dos valores lógicos das preposições simples, e mais adiante veremos como determinar o valor lógico de uma proposição composta.

Proposição composta do tipo P(p, q)



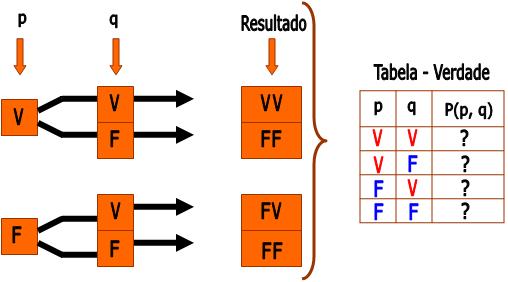
Proposição composta do tipo P(p, q, r)



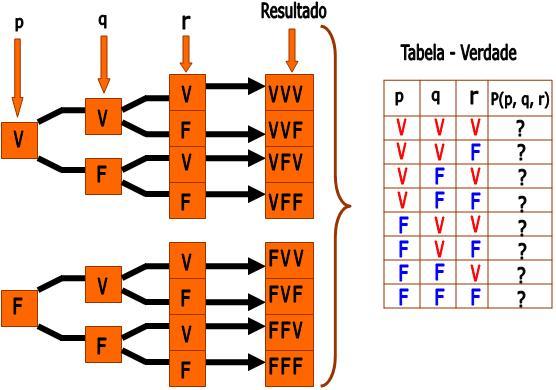
Proposição composta do tipo P(p, q, r, s)

A tabela-verdade possui 2⁴ = 16 linhas e é formada igualmente as anteriores.



Proposição composta do tipo P(p1, p2, p3,..., pn)

A tabela-verdade possui 2ⁿ linhas e é formada igualmente as anteriores.

Tabela-Verdade de uma proposição composta

Exemplo

Veja como se procede a construção de uma tabela-verdade da proposição composta P(p, q) = ((p ⋁ q) → (~p)) → (p ⋀ q), onde p e q são duas proposições simples.

Resolução

Uma tabela-verdade de uma proposição do tipo P(p, q) possui 2⁴ = 4 linhas, logo:



Agora veja passo a passo a determinação dos valores lógicos de P.

a) Valores lógicos de p ν q



b) Valores lógicos de ~p



c) Valores lógicos de (p ν q) → (~p)




d) Valores lógicos de p Λ q



e) Valores lógicos de P(p, q) = ((p ν q) → (~p)) → (p Λ q)

Tautologia, contradição e contingência

Tautologia

Tautologia é uma proposição cujo valor lógico é sempre verdadeiro.

Exemplo

A proposição p ∨ (~p) é uma tautologia, pois o seu valor lógico é sempre V, conforme a tabela-verdade.



Exemplo

A proposição (p Λ q) → (p → q) é uma tautologia, pois a última coluna da tabela-verdade só possui V.



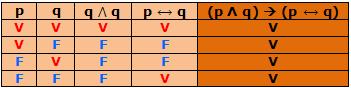
Contradição

Contradição é uma proposição cujo valor lógico é sempre falso.

Exemplo

A proposição (p Λ q) Λ (p Λ q) é uma contradição, pois o seu valor lógico é sempre F conforme a tabela-verdade. Que significa que uma proposição não pode ser falsa e verdadeira ao mesmo tempo, isto é, o principio da não contradição.



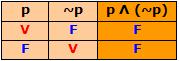
Exemplo

A proposição ~(p ν q) Λ (p Λ q) é contraválida, pois a última coluna da tabela-verdade só possui F.



Contingência

Quando uma proposição não é tautológica nem contraválida, a chamamos de contingência ou proposição contingente ou proposição indeterminada.

Teorema contra-recíproco

A equivalência (p → q) ⇔ (~q → ~p), tem o seguinte significado:

Sendo p → q = V, nesse caso:

p ⇒ q é equivalente a (~q) ⇒ (~p)

Exemplo

b = 8 ⇒ b > 3 é equivalente a b <> ⇒ b ≠ 8

Valor lógico

Considerando os princípios citados acima, uma proposição é classificada como verdadeira ou falsa.

Sendo assim o valor lógico será:

- a verdade (V), quando se trata de uma proposição verdadeira.

- a falsidade (F), quando se trata de uma proposição falsa

Ensino Fundamental - Divisão

DIVISÃO

A operação divisão está ligado à idéia de repartir uma quantidade em partes iguais e à idéia de verificar quantas vezes uma quantidade cabe em outra.A divisão é a operação inversa da multiplicação. Os termos da divisão chamam-se dividendo e divisor e, o resultado da operação, quociente.

Técnicas Operatórias

Exemplo 01 Dividendo Divisor Quociente 8 : 4 = 2

Exemplo 02 46,87 |5,2 1) Igualar as casas decimais do dividendo e/ou divisor, acrescentando com Zeros (0) onde for o caso. 2) Cortar as vírgulas e efetuar a operação. Dividendo 46,87 |5,20 - Divisor - 468 9,01 - Quociente 0700 - 520 180 - Resto

Exemplo 03 783,5 |8,16 78350 |816 - 7344 96,01 4910 - 4896 1400 - 816 584

Exemplo 04 7,36 |0,5 736 |50 -50 14,72 236 -200 360 -350 100 -100 0

Exemplo 05 435 |762 4350 |762 -3810 0,57 5400 -5334 66

Exemplo 06 10201 |101 - 101 101 101 - 101 0 Fonte:http://adasantanna.vilabol.uol.com.br/

Ensino Fundamental - Multiplicação

MULTIPLICAÇÃO

A multiplicação é uma operação que pode estar associada à idéias de juntar quantidades iguais ou à idéia combinatória. Os termos da multiplicação chamam-se fatores e o resultado da operação, produto. O 1º fator é também conhecido como multiplicando e o 2º, como multiplicador.

Técnicas Operatórias

Exemplo 01 Multiplicando Multiplicador Produto 5.2 = 10

Exemplo 02 13,25 - 2 ordens decimais x 50,7 - 1 ordem decimal + 9275 6625 671,775 - 3 ordens decimais Seiscentos e setenta e um inteiros, setecentos e setenta e cinco milésimos (leitura por extenso). Exemplo 03 4567 - Multiplicando x 8,09 - Multiplicador + 41103 - 1º P. Parcial 36536 _ - 2º P. Parcial 36947,03 - Produto Final 3 - Centésimo 0 - Décimo 7 - Unidade Inteira ou Simples 4 - Dezena 9 - Centena 6 - Unidade de Milhar 3 - Dezena de Milhar Fonte:http://adasantanna.vilabol.uol.com.br/

Ensino Fundamental-Subtração

SUBTRAÇÃO

A subtração é uma operação que pode estar associada a três idéias diferentes:Tirar, Completar ou Comparar.A subtração é a operação inversa da adição. Os termos da subtração chamam-se minuendo e subtraendo e o resultado da operação, resto ou diferença.

Técnicas Operatórias

Exemplo 01 Minuendo Subtraendo Resto 8 - 3 = 5

Exemplo 02 86,97 - 3,6 - 11,13 = 1) Colocar vírgula debaixo de vírgula. 2) Completar com zeros e efetuar a operação. 86,97 - Minuendo - 3,60 - Subtraendo 11,13 - Subtraendo 72,24 - Resto e/ou Diferença 86,97 3,60 83,37 86,97 - 3,60 + 11,13 - 11,13 - 14,73 83,37 14,73 72,24 72,24 Setenta e dois inteiros e vinte e quatro centésimo (leitura por extenso). Fonte:http://adasantanna.vilabol.uol.com.br/

Ensino Fundamental- Adição

ADIÇÃO

A adição é uma operação ligada a situações que envolvem as ações de juntar ou

acrescentar quantidades. Os termos da adição chamam-se parcelas e o

resultado da operação, soma ou total.

Técnicas Operatórias

Exemplo 01 1ª parcela 2ª parcela Soma 8 + 3 = 11

Exemplo 02 3,07 + 5 + 2,53 = 1) Colocar vírgula debaixo de vírgula: 3,07 + 5 2,53 2) Completar com zeros e efetuar a operação: 3,07 - 1ª parcela + 5,00 - 2ª parcela 2,53 - 3ª parcela 10,60 - Soma e/ou Total Dez inteiros e sessenta centésimos (leitura por extenso) Fonte:http://adasantanna.vilabol.uol.com.br/

Congruência e Semelhança de Triângulos

Temos que dois triângulos são congruentes:
Quando seus elementos (lados e ângulos) determinam a congruência entre os triângulos.
Quando dois triângulos determinam a congruência entre seus elementos.

Casos de congruência:

1º LAL (lado, ângulo, lado): dois lados congruentes e ângulos formados também congruentes.


2º LLL (lado, lado, lado): três lados congruentes.

3º ALA (ângulo, lado, ângulo): dois ângulos congruentes e lado entre os ângulos congruente.

4º LAA (lado, ângulo, ângulo): congruência do ângulo adjacente ao lado, e congruência do ângulo oposto ao lado.

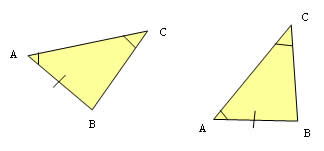
Através das definições de congruência de triângulos podemos chegar às propriedades geométricas sem a necessidade de efetuar medidas. A esse método damos o nome de demonstração.
Dizemos que em todo triângulo isósceles, os ângulos opostos aos lados congruentes são congruentes. Os ângulos da base de um triângulo isósceles são congruentes.

Poesia Matemática

Poesia Matemática

Millôr Fernandes


Às folhas tantas
do livro matemático
um Quociente apaixonou-se
um dia
doidamente
por uma Incógnita.
Olhou-a com seu olhar inumerável
e viu-a do ápice à base
uma figura ímpar;
olhos rombóides, boca trapezóide,
corpo retangular, seios esferóides.
Fez de sua uma vida
paralela à dela
até que se encontraram
no infinito.
"Quem és tu?", indagou ele
em ânsia radical.
"Sou a soma do quadrado dos catetos.
Mas pode me chamar de Hipotenusa."
E de falarem descobriram que eram
(o que em aritmética corresponde
a almas irmãs)
primos entre si.
E assim se amaram
ao quadrado da velocidade da luz
numa sexta potenciação
traçando
ao sabor do momento
e da paixão
retas, curvas, círculos e linhas sinoidais
nos jardins da quarta dimensão.
Escandalizaram os ortodoxos das fórmulas euclidiana
e os exegetas do Universo Finito.
Romperam convenções newtonianas e pitagóricas.
E enfim resolveram se casar
constituir um lar,
mais que um lar,
um perpendicular.
Convidaram para padrinhos
o Poliedro e a Bissetriz.
E fizeram planos, equações e diagramas para o futuro
sonhando com uma felicidade
integral e diferencial.
E se casaram e tiveram uma secante e três cones
muito engraçadinhos.
E foram felizes
até aquele dia
em que tudo vira afinal
monotonia.
Foi então que surgiu
O Máximo Divisor Comum
freqüentador de círculos concêntricos,
viciosos.
Ofereceu-lhe, a ela,
uma grandeza absoluta
e reduziu-a a um denominador comum.
Ele, Quociente, percebeu
que com ela não formava mais um todo,
uma unidade.
Era o triângulo,
tanto chamado amoroso.
Desse problema ela era uma fração,
a mais ordinária.
Mas foi então que Einstein descobriu a Relatividade
e tudo que era espúrio passou a ser
moralidade
como aliás em qualquer
sociedade.

Texto extraído do livro "Tempo e Contratempo", Edições O Cruzeiro - Rio de Janeiro, 1954, pág. sem número, publicado com o pseudônimo de Vão Gogo.

Tudo sobre Millôr Fernandes e sua obra em "Biografias".