As inequações são expressões matemáticas que utilizam na sua formatação, os seguintes sinais de desigualdades:
>: maior que
<: menor que
≥: maior ou igual
≤: menor ou igual
≠: diferente
Exemplo 1
Vamos resolver a inequação 3x² + 10x + 7 <>.


S = {x Є R / –7/3 < x < –1}
Exemplo 2
Determine a solução da inequação –2x² – x + 1 ≤ 0.


S = {x Є R / x < –1 ou x > 1/2}
Exemplo 3
Determine a solução da inequação x² – 4x ≥ 0.
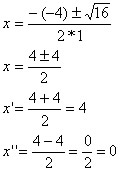
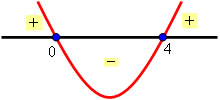
S = {x Є R / x ≤ 0 ou x ≥ 4}
Exemplo 4
Calcule a solução da inequação x² – 6x + 9 > 0.
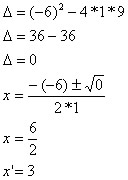
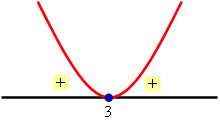
Uma inequação será identificada como modular se dentro do módulo tiver uma expressão com uma ou mais incógnitas, veja alguns exemplos de inequações modulares:
|x| > 5
|x| < 5
|x – 3| ≥ 2
Condição de existência de um módulo, considerando k um número real positivo:
Se |x| < k então, – k < x < k
Se |x| > k então, x < – k ou x > k
Exemplo 1
|x| ≤ 6
Utilizando a seguinte definição: se |x| < k então, – k < x < k, temos que:
– 6 ≤ x ≤ 6

S = {x Є R / – 6 ≤ x ≤ 6}
Exemplo 2
|x – 7| <>
Utilizando a seguinte definição: se |x| < k então, – k < x < k, temos que:
– 2 < x – 7 < 2
– 2 + 7 < x < 2 + 7
5 <>

Exemplo 3
|x² – 5x | > 6
Precisamos verificar as duas condições:
|x| > k então, x < – k ou x > k
|x| < k então, – k < x < k
Fazendo |x| > k então, x < – k ou x > k
x² – 5x > 6
x² – 5x – 6 > 0
Aplicando Bháskara temos:
x’ = 6
x” = –1
Pela propriedade:
x > 6
x < –1
Fazendo |x| < k então, – k < x < k
x² – 5x < – 6
x² – 5x + 6 < 0
Aplicando Bháskara temos:
x’ = 3
x” = 2
Pela propriedade:
x > 2
x < 3
S = {x Є R / x < –1 ou 2 <> 6}.
9 comentários:
bacana viu
muito bom , essas explicações me ajudaram a entender e muito
BACANÍSSIMO O SITE ! Parabéns, me ajudou muito !:D
muito bom esse site!, me ajudou muito nas revisões da faculdade.
Obrigada :)
muito bom esse site!, me ajudou muito nas revisões da faculdade.
Obrigada :)
super bacana o site ,uma bela forcinha para nós. Obg !
ajudou bastante :) parabéns pelo site
imuito legal essas explicaçoes mt bacana mesmo ...
so faltou os gráficos, mas o post é muito bom, parabéns!
Postar um comentário