EQUAÇÕES BIQUADRADAS

EQUAÇÕES BIQUADRADAS

Observe as equações:

x⁴ - 13x² + 36 = 0

9x⁴ - 13x² + 4 = 0

x⁴ - 5x² + 6 = 0

Note que os primeiros membros são polinômios do 4º grau na variável x, possuindo um termo em x⁴, um termo em x² e um termo constante. Os segundos membros são nulos.

Denominamos essas equações de equações biquadradas.

Ou seja, equação biquadrada com uma variável x é toda equação da forma:

ax4 + bx2 + c = 0

Exemplos:

x⁴ - 5x² + 4 = 0

x⁴ - 8x² = 0

3x⁴ - 27 = 0

Cuidado!

x⁴ - 2x³ + x² + 1 = 0 6x⁴ + 2x³ - 2x = 0 x⁴ - 3x = 0

As equações acima não são biquadradas, pois numa equação biquadrada a variável x só possui expoentes pares.

RESOLUÇÃO DE UMA EQUAÇÃO BIQUADRADA

Na resolução de uma equação biquadrada em IR devemos substituir sua variável, transformando-a numa equação do 2º grau.

Observe agora a sequência que deve ser utilizada na resolução de uma equação biquadrada.

Seqüência prática

• Substitua x⁴ por y² ( ou qualquer outra incógnita elevada ao quadrado) e x² por y.

• Resolva a equação ay² + by + c = 0

• Determine a raiz quadrada de cada uma da raízes ( y'e y'') da equação ay² + by + c = 0.

Essas duas relações indicam-nos que cada raiz positiva da equação ay² + by + c = 0 dá origem a duas raízes simétricas para a biquadrada: a raiz negativa não dá origem a nenhuma raiz real para a mesma.

Exemplos:

• Determine as raízes da equação biquadrada x⁴ - 13 x² + 36 = 0.

Solução

Substituindo x⁴ por y² e x² por y, temos:

y² - 13y + 36 = 0

Resolvendo essa equação, obtemos:

y'=4 e y''=9

Como x²= y, temos:

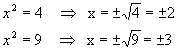
Logo, temos para conjunto verdade: V={ -3, -2, 2, 3}.

• Determine as raízes da equação biquadrada x⁴ + 4x² - 60 = 0.

Solução

Substituindo x⁴ por y² e x² por y, temos:

y² + 4y - 60 = 0

Resolvendo essa equação, obtemos:

y'=6 e y''= -10

Como x²= y, temos:

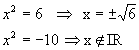
Logo, temos para o conjunto verdade:.

• Determine a soma das raízes da equação .

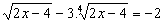Solução

Utilizamos o seguinte artifício:

Assim:

y² - 3y = -2

y² - 3y + 2 = 0

y'=1 e y''=2

Substituindo y, determinamos:

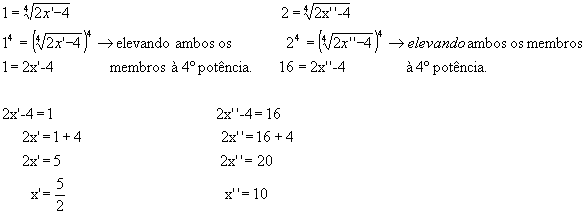
Logo, a soma das raízes é dada por:

Resolução de equações da forma: ax²ⁿ + bxⁿ + c = 0

Esse tipo de equação pode ser resolvida da mesma forma que a biquadrada.

Para isso, substituimos xⁿ por y, obtendo:

ay² + by + c = 0, que é uma equação do 2º grau.

Exemplo:

• resolva a equação x⁶ + 117x³ - 1.000 = 0.

Solução

Fazendo x³=y, temos:

y² + 117y - 1.000 = 0

Resolvendo a equação, obtemos:

y'= 8 e y''= - 125

Então:

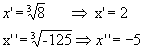
Logo, V= {-5, 2 }.

Composição da equação biquadrada

Toda equação biquadrada de raízes reais x₁, x₂, x₃ e x₄ pode ser composta pela fórmula:

(x -x1) . (x - x2) . (x - x3) . (x - x4) = 0

Exemplo:

• Compor a equação biquadrada cujas raízes são:

Solução

a) (x - 0) (x - 0) (x + 7) (x - 7) = 0 b) (x + a) (x - a) (x + b) (x - b) = 0

x²(x² -49) = 0 (x²-a²) (x²-b²) = 0

x⁴ - 49x² = 0 x⁴ - (a² + b²) x² + a²b² = 0

PROPRIEDADES DAS RAÍZES DA EQUAÇÃO BIQUADRADA

Consideremos a equação ax⁴ + bx² + c = 0, cujas raízes são x₁, x₂, x₃ e x₄ e a equação do 2º grau ay² + by + c = 0, cujas raízes são y' e y''.

De cada raiz da equação do 2º grau, obtemos duas raízes simétricas para a biquadrada. Assim:

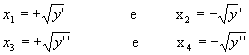
Do exposto, podemos estabelecer as seguintes propriedades:

1ª Propriedade: A soma das raízes reais da equação biquadrada é nula.

x1 + x2 + x3 + x4 = 0

2ª Propriedade: A soma dos quadrados das raízes reais da equação biquadrada é igual a -.

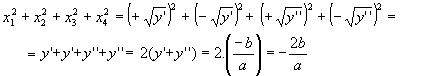
3ª Propriedade:O produto das raízes reais e não-nulas da equação biquadrada é igual a .