Pertencem ao conjunto dos naturais os números inteiros positivos incluindo o zero. Representado pela letra N maiúscula. Os elementos dos conjuntos devem estar sempre entre chaves.
N = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, ... }
- Quando for representar o Conjunto dos Naturais não – nulos (excluindo o zero) devemos colocar * ao lado do N.
Representado assim:
N* = {1, 2,3 ,4 ,5 ,6 ,7 ,8 ,9 ,10 ,11 ,12, ... }
A reticência indica que sempre é possível acrescentar mais um elemento.
N = {0, 1, 2, 3, 4, 5, 6, ...} ou N = {0, 1, 2, 3, 4, 5, 6, 7, ... }
Qualquer que seja o elemento de N, ele sempre tem um sucessor. Também falamos em antecessor de um número.
• 6 é o sucessor de 5.
• 7 é o sucessor de 6.
• 19 é antecessor de 20.
• 47 é o antecessor de 48.
Como todo número natural tem um sucessor, dizemos que o conjunto N é infinito.
Quando um conjunto é finito?
O conjunto dos números naturais maiores que 5 é infinito: {6, 7, 8, 9, ...}
Já o conjunto dos números naturais menores que 5 é finito: {0, 1, 2, 3, 4}
Veja mais alguns exemplos de conjuntos finitos.
• O conjunto dos alunos da classe.
• O conjunto dos professores da escola.
• O conjunto das pessoas que formam a população brasileira.
Interseção do conjunto dos naturais e dos inteiros.
N = { 0,1,2,3,4,5,6, ... }
Z = { ... , -3,-2,-1,0,1,2,3,4, ... }
N![]() Z
Z
►Os números inteiros são encontrados com freqüência em nosso cotidiano, por exemplo:
♦ Exemplo 1: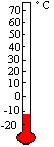
Quando falamos acima de zero, estamos nos referindo aos números positivos e quando falamos dos números abaixo de zero estamos referindo aos números negativos.
+10° C ------------- 10° C acima de zero
- 3° C --------------- 3° C abaixo de zero
♦ Exemplo 2:
• dos R$500,00 retira R$200,00 e fica com R$300,00
• dos R$300,00 retira R$200,00 e fica com R$100,00
• dos R$100,00 retira R$200,00 e fica devendo R$ 100,00
A última retirada fez com que a pessoa ficasse devendo dinheiro ao banco. Assim:
Dever R$100,00 significa ter R$100,00 menos que zero. Essa dívida pode ser representada por – R$100,00.
►Oposto de um número inteiro
►O conjunto dos números inteiros possui alguns subconjuntos:
- Inteiros não – nulos
São os números inteiros, menos o zero.
Na sua representação devemos colocar * ao lado do Z.
Z* = {..., -3, -2, -1, 1, 2, 3,...}
- Inteiros não positivos
São os números negativos incluindo o zero.
Na sua representação deve ser colocado - ao lado do Z.
Z_ = {..., -3, -2, -1, 0}
- Inteiros não positivos e não – nulos
São os números inteiros do conjunto do Z_ excluindo o zero.
Na sua representação devemos colocar o _ e o * ao lado do Z.
Z*_ = {..., -3, -2, -1}
- Inteiros não negativos
São os números positivos incluindo o zero.
Na sua representação devemos colocar o + ao lado do Z.
Z + = { 0,1 ,2 ,3, 4,...}
O Conjunto Z + é igual ao Conjunto dos N
- Inteiros não negativos e não - nulos
São os números do conjunto Z+, excluindo o zero.
Na sua representação devemos colocar o + e o * ao lado do Z.
Z* + = {1, 2, 3, 4,...}
O Conjunto Z* + é igual ao Conjunto N*
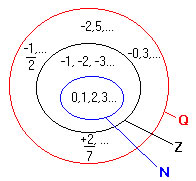
Interseção dos conjuntos: Naturais, Inteiros e Racionais.
Os números decimais são aqueles números que podem ser escritos na forma de fração.
Podemos escrevê-los de algumas formas diferentes:
Por exemplo:
♦ Em forma de fração ordinária: ![]() ;
; ![]() ;
;![]() e todos os seus opostos.
e todos os seus opostos.
Esses números tem a forma ![]() com a , b
com a , b ![]() Z e b ≠ 0.
Z e b ≠ 0.
♦ Números decimais com finitas ordens decimais ou extensão finita:
Esses números têm a forma 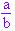 com a , b
com a , b 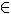 Z e b ≠ 0.
Z e b ≠ 0.
♦ Número decimal com infinitas ordens decimais ou de extensão infinita periódica. São dízimas periódicas simples ou compostas:
As dízimas periódicas de expansão infinita, que podem ser escritas na forma ![]() : com a, b
: com a, b 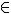 Z e b ≠ 0.
Z e b ≠ 0.
► O conjunto dos números racionais é representado pela letra Q maiúscula.
Q = {x = ![]() , com a Z e b Z*}
, com a Z e b Z*}

►Outros subconjuntos de Q:
Além de N e Z, existem outros subconjuntos de Q.
Q* ---------- É o conjunto dos números racionais diferentes de zero.
Q+ ---------- É o conjunto dos números racionais positivos e o zero.
Q- ----------- É o conjunto dos números racionais negativos e o zero.
Q*+ ---------- É o conjunto dos números racionais positivos.
Q*- ----------- É o conjunto dos números racionais negativos.
► Representação Geométrica
Entre dois números racionais existem infinitos outros números racionais.
Por Danielle de Miranda
Graduada em Matemática
Equipe Brasil Escola
22 comentários:
oi bom dia!! queria parabeniza-lo pois gostei muito de sua apresentao,tirei as duvidas q tinha e rapido.
agradeco.
eu não entendi nada
"Seria bom alguns exercícios respondidos passo a passo."
" Seria bom alguns exercícios resolvidos passo a passo."
que bom essa aula gosto muito de matemática
Olá! bom dia! Primeiramente gostaria de Parabeniza-lo pelo blog, e dizer que consegui tirar as duvidas que eu tinha. rs
Mas gostaria de pedir, se possível, alguns exercícios que resolvidos para clarear ainda mais as nossas dúvidas.
Desde já, Obrigada!
da pra entender tudinho ... mas vc precisa deixar claro o que é pertence, nao pertence ...
pq tem gente que nao sabe o que é !
mas ta de parabéns
Muito bom.
Simples, prático e objetivo... interessante !
parabens pela atitude de ajudar,com metodo bem simples e claro.gostei muito.obrigado.
OI Muito obrigada mesmo! Minha professora descidiu dar uma prova do nada e eu tinha lido isso e era exatamente o mesmo tirei 9:P obg mesmo!!!
amei fiz um trabalho sobre o assunto basiado na sua explicaçao ficou mara bjs
Muito obrigado, vou ter as provas nacionais e tirei algumas duvidas. obrigado. :)
Finalmente depois de anos encontrei alguém que passe uma explicação mais fácil e concreta sobre a questão dos sinais. Mais com menos, menos com mais e seus resultados. Muito agradecida mesmo e novamente parabéns.
Atenciosamente
Gabriela M. C. M.
UNIP Vergueiro CB
Finalmente depois de anos encontrei alguém que passe uma explicação mais fácil e concreta sobre a questão dos sinais. Mais com menos, menos com mais e seus resultados. Muito agradecida mesmo e novamente parabéns.
Atenciosamente
Gabriela M. C. M.
UNIP Vergueiro CB
gostei bem facil a explicação,mas pra enteder melhor e não ficar nenhuma duvida vou ler mas algumas vezes.
muito bom mesmo, parabens.
Demais!!! Ótima explicação!
gostei muito otima esplicação aprendi muito !
Adorei a sua apresentação.. estou estudando para concurso, e sua explicação ajudou bastante..
hum me ajudou muito amanha vou ter uma prova e agora sei tudinho !
Parabéns ... A prof ensinou um dia na escola i eu não tinha intendido nada pois ela me explicou d uma forma totalmente diferente , ae dps de uma semana resolvi pesquisar e intendi perfeitamente ... só não intendi quais são os n° racionais exatamente(os números reais que ainda não aprendi) .. mais vou perguntar pra outra prof d matematica i ela me fala rsrsrs bgd mesmo , tudo em dobro
Explicação mt clara, obg. Me ajudou bastante!
Postar um comentário