Pares ordenados

Pares ordenados

Muitas vezes, para localizar um ponto num plano, utilizamos dois números racionais, numa certa ordem.

Denominamos esses números de par ordenado. Exemplos:

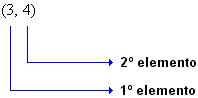
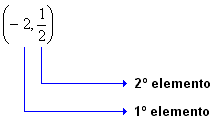
Assim:

Indicamos por (x, y) o par ordenado formado pelos elementos x e y, onde x é o 1º elemento e y é o 2º elemento.

• Observações

1. De um modo geral, sendo x e y dois números racionais quaisquer, temos: 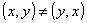. Exemplos

2. Dois pares ordenados (x, y) e (r, s) são iguais somente se x = r e y = s.

Representação gráfica de um Par Ordenado

Podemos representar um par ordenado através de um ponto em um plano.

Esse ponto é chamado de imagem do par ordenado.

Coordenadas Cartesianas

Os números do par ordenados são chamados coordenadas cartesianas. Exemplos:

A (3, 5) ==> 3 e 5 são as coordenadas do ponto A.

Denominamos de abscissa o 1º número do par ordenado, e ordenada, o 2º número desse par. Assim:

Plano Cartesiano

Representamos um par ordenado em um plano cartesiano. Esse plano é formado por duas retas, x e y, perpendiculares entre si. A reta horizontal é o eixo das abscissas (eixo x). A reta vertical é o eixo das ordenadas (eixo y). O ponto comum dessas duas retas é denominado origem, que corresponde ao par ordenado (0, 0).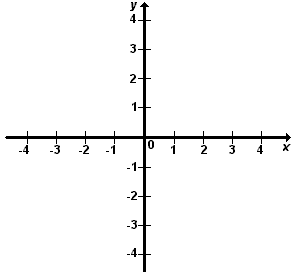

Localização de um Ponto

Para localizar um ponto num plano cartesiano, utilizamos a seqüência prática:

• O 1º número do par ordenado deve ser localizado no eixo das abscissas.

• O 2º número do par ordenado deve ser localizado no eixo das ordenadas.

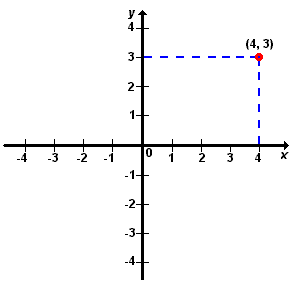
• No encontro das perpendiculares aos eixos x e y, por esses pontos, determinamos o ponto procurado. Exemplo:

• Localize o ponto (4, 3).

Produto Cartesiano

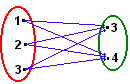
Sejam os conjuntos A = {1, 2, 3} e B = {3, 4}. Com auxílio do diagrama de flechas ao lado formaremos o conjunto de todos os pares ordenados em que o 1º elemento pertença ao conjunto A e o 2º pertença ao conjunto B.

Assim , obtemos o conjunto: {(1, 3), (1, 4), (2, 3), (2, 4), (3, 3), (3, 4)}

Esse conjunto é denominado produto cartesiano de A por B, e é indicado por:

Logo:

Dados dois conjuntos A e B, não-vazios, denominamos produtos cartesiano A x B o conjunto de todos os pares ordenados (x, y) onde

Fonte sómatematica