sexta-feira, 30 de dezembro de 2011
terça-feira, 27 de dezembro de 2011
segunda-feira, 26 de dezembro de 2011
Numeração decimal IV
As figuras foram divididas em 10 e 100 pares, respectivamente. A seguir foram coloridas de verde escuro 4 e 40 destas parte, respectivamente. Observe:
 |  |
Logo, decimais equivalentes são aqueles que representam a mesma quantidade.
Exemplos:
| 0,4 = 0,40 = 0,400 = 0,4000 | 8 = 8,0 = 8,00 = 8,000 |
| 2,5 = 2,50 = 2,500 = 2,5000 | 95,4 = 95,40 = 95,400 = 95,4000 |
| Um número não se altera quando se acrescenta ou se suprime um ou mais zeros à direita de sua parte decimal. |
Comparar dois números decimais significa estabelecer uma relação de igualdade ou de desigualdade entre eles. Consideremos dois casos:
1º Caso: As partes inteira
O maior é aquele que tem a maior parte inteira.
|
O maior é aquele que tem a maior parte decimal. É necessário igualar inicialmente o número de casas decimais acrescentando zeros.
|
- 0,75 > 0,7 ou 0,75 > 0,70 (igualando as casas decimais), pois 75 > 70.
- 8,3 > 8,03 ou 8,30 > 8,03 (igualando as casas decimais ), pois 30 > 3.
Numeração decimal
Numeração decimal
Transformação de números decimais em frações decimais
Observe os seguintes números decimais:
-
0,8 (lê-se "oito décimos"), ou seja,
. -
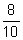0,65 (lê-se "sessenta e cinco centésimos"), ou seja,
. -
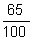5,36 (lê-se "quinhentos e trinta e seis centésimos"), ou seja,
. -
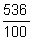0,047 (lê-se "quarenta e sete milésimos"), ou seja,
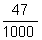
Verifique então que:
 |  |
 |  |
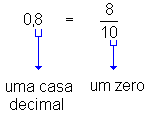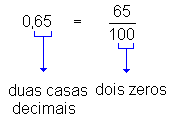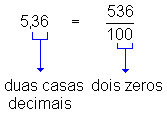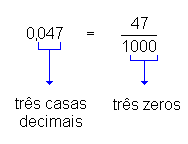Assim:
| Um número decimal é igual à fração que se obtém escrevendo para numerador o número sem vírgula e dando para denominador a unidade seguida de tantos zeros quantas forem as casas decimais. |
Transformação de fração decimal em número decimal
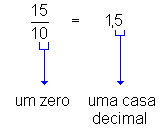
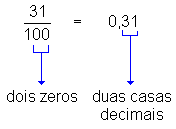
Observe as igualdades entre frações decimais e números decimais a seguir:
 |  |
 |  |
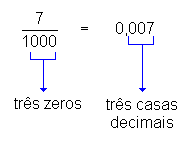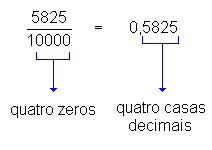Podemos concluir, então, que:
Para se transformar uma fração decimal em número decimal, basta dar ao numerador tantas casas decimais quantos forem os zeros do denominador.fonte :http://www.somatematica.com.br
Numeração decimal III
Numeração decimal
Leitura dos números decimais
No sistema de numeração decimal, cada algarismo, da parte inteira ou decimal, ocupa uma posição ou ordem com as seguintes denominações:
| ||||||||||||||||||
Leitura
Lemos a parte inteira, seguida da parte decimal, acompanhada das palavras:
décimos ........................................... : quando houver uma casa decimal;
centésimos....................................... : quando houver duas casas decimais;
milésimos......................................... : quando houver três casas decimais;
décimos milésimos ........................ : quando houver quatro casas decimais;
centésimos milésimos ................... : quando houver cinco casas decimais e, assim sucessivamente.
Exemplos:
1,2: um inteiro e dois décimos;
2,34: dois inteiros e trinta e quatro centésimos
Quando a parte inteira do número decimal é zero, lemos apenas a parte decimal.
Exemplos:
0,1 : um décimo;
0,79 : setenta e nove centésimos
Observação:
1. Existem outras formas de efetuar a leitura de um número decimal. Observe a leitura do número 5,53:
Leitura convencional: cinco inteiros e cinquenta e três centésimos;
Outras formas: quinhentos e cinquenta e três centésimos;
cinco inteiros, cinco décimos e três centésimos.
2. Todo números natural pode ser escrito na forma decimal, bastando colocar a vírgula após o último algarismo e acrescentar zero(s). Exemplos:
4 = 4,0 = 4,00 75 = 75,0 = 75,00
fonte :http://www.somatematica.com.brNumeração decimal II
Numeração decimal
Números Decimais
O francês Viète (1540 - 1603) desenvolveu um método para escrever as frações decimais; no lugar de frações, Viète escreveria números com vírgula. Esse método, modernizado, é utilizado até hoje.
Observe no quando a representação de frações decimais através de números decimais:
| Fração Decimal | = | Números Decimais |
 | = | 0,1 |
 | = | 0,01 |
 | = | 0,001 |
 | = | 0,0001 |
| Fração Decimal | = | Números Decimais |
 | = | 0,5 |
 | = | 0,05 |
 | = | 0,005 |
 | = | 0,0005 |
| Fração Decimal | = | Números Decimais |
 | = | 11,7 |
 | = | 1,17 |
 | = | 0,117 |
 | = | 0,0117 |
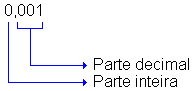
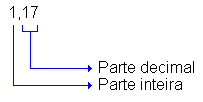
Os números 0,1, 0,01, 0,001; 11,7, por exemplo, são números decimais.
Nessa representação, verificamos que a vírgula separa a parte inteira da parte decimal.
|
|
|
Numeração decimal
Numeração decimal
Introdução
A figura nos mostra um paralelepípedo com suas principais dimensões em centímetros.
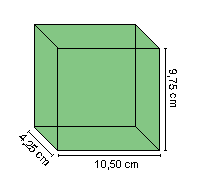
Essas dimensões são apresentadas sob a forma de notação decimal, que corresponde a uma outra forma de representação dos números racionais fracionários.
A representação dos números fracionária já era conhecida há quase 3.000 anos, enquanto a forma decimal surgiu no século XVI com o matemático francês François Viète.
O uso dos números decimais é bem superior ao dos números fracionários. Observe que nos computadores e nas máquinas calculadoras utilizamos unicamente a forma decimal.
Frações Decimais
Observe as frações:
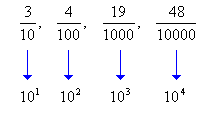
Os denominadores são potências de 10.
Assim:
Denominam-se frações decimais, todas as frações que apresentam potências de 10 no denominador.fonte :http://www.somatematica.com.br