Um método para calcular o MMC e MDC entre dois números

Neste post, apresento um método onde podemos calcular o mmc e o mdc entre dois números inteiros sem fazer contas utilizando papel quadriculado e uma régua. Vejamos os procedimentos:

MMC

Considere os dois números inteiros que desejamos determinar seu mmc. Num papel quadriculado, desenhe o contorno de um retângulo com dimensões a e b. De qualquer um dos vértices deste retângulo, trace diagonais nos quadradinho internos, só finalizando quando encontrar um novo vértice. Conte quantas diagonais foram traçadas. Esse número é o mmc procurado.

Exemplos:

1) Vamos determinar o mmc entre 2 e 3: Desenhamos o contorno de um retângulo com dimensões 2 e 3 e traçamos diagonais nos quadradinhos internos partindo de um dos vértices do retângulo:

Vejam que foram traçadas seis diagonais que equivale a dizer que 6 é o mmc entre os números 2 e 3.

2) Vamos determinar o mmc entre 3 e 5: Utilizando o mesmo procedimento, obtemos:

Vejam que foram traçadas quinze diagonais que equivale dizer que 15 é o mmd entre os números 3 e 5.

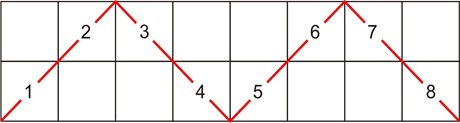
3) Vamos determinar o mmc entre 2 e 8 utilizando o mesmo procedimento:

MDC

Considere os dois números inteiros que desejamos determinar seu mdc. Num papel quadriculado, desenhe o contorno de um retângulo com dimensões a e b. Partindo de qualquer um dos vértices, trace uma diagonal do retângulo. Sempre que esta diagonal encontrar com um vértice de um dos quadradinhos internos, marque com um ponto. Em seguida, conte em quantas partes a diagonal do retângulo foi dividida. Este número é o mdc procurado.

Exemplos:

4) Vamos determinar o mdc entre 2 e 3: Desenhamos o contorno de um retângulo com dimensões 2 e 3 e traçamos uma diagonal do retângulo:

Vejam que a diagonal traçada encontra somente dois vértices dos quadradinhos internos. Então esta diagonal foi dividida em 1 parte. Esse número de divisões da diagonal é equivalente ao mdc entre os número 2 e 3.

5) Vamos determinar o mdc entre os números 2 e 4 utilizando o mesmo procedimento:

Vejam que a diagonal traçada encontra três vértices dos quadradinhos internos. Então esta diagonal foi dividida em 2 partes. Esse número de divisões da diagonal é equivalente ao mdc entre os número 2 e 4.

6) Vamos determinar o mdc entre os números 4 e 10 utilizando o mesmo procedimento:

Vejam que a diagonal traçada encontra três vértices dos quadradinhos internos. Então esta diagonal foi dividida em 2 partes. Esse número de divisões da diagonal é equivalente ao mdc entre os número 4 e 10.

Podemos trabalhá-lo em sala de aula de modo a explorar o desenvolvimento geométrico pelos alunos.

Creio que já “pegamos o jeito” da coisa e dispensa mais exemplos. Caso haja alguma dúvida no método, entre em contato.

Fonte: http://obaricentrodamente.blogspot.com/2010/02/um-metodo-para-calcular-o-mmc-e-mdc.html